最強「かけ算テク」4つ おそらく、こういった計算方法をなんとなくは知りつつも、しっかり使いこなせるほどマスターしている人は少ないのではないでしょうか? 今日こそ、そのきっかけの日になるかもしれません。 ここで紹介するのは、米メディア筆算のイメージを持ちやすくする。 本単元では、(2,3位数×2位数)の かけ算の意味や計算の仕方を考え、理 解した上で、筆算の仕方を定着させる ことを目指している。筆算の定着を図 るには、機械的な作業としての筆算だ知識・理解 ・2~3位数×2位数の乗法の筆算の仕方について理解する。 第2学年 11)かけ算(1) ・かけ算の意味 12)かけ算(2) ・九九の完成 算と筆算形式 ・交換法則 ・分配法則 ・九九表のきまり ・倍の第三用法 第3学年 1) かけ算 ・分配法則の活用 ・
算数4年から6年
かけ算 の 筆算 の 仕方
かけ算 の 筆算 の 仕方-の筆算の仕方を考える。 第3時ーの位に繰り上がりがある(2桁) x (1桁)の筆算の仕方を考える。 第4時十の位に繰り上がりがある(2桁) x (1桁)の筆算の仕方を考える。 第5時繰り上がりが2回ある(2桁)x (1 桁)の筆算の仕方を考える。 第6時 (2桁)x (1桁)の筆算の習熟を3などの筆算の仕方を 考える。 (本時) ・2位数×1位数の筆算の仕方に着 目して,3位数×1位数の筆算の 仕方を考え,説明している。 行動観察 評価問題 9 ・既習の乗法などに着目 して386×2や937×4 などの筆算の仕方を考 える。 ・




12 小学2 3年生の算数 大きい数の掛け算 掛け算の筆算のやり方はくり上がりに気を付けよう 無料学習 掛け算3時間目 キッキブログ なんで を探す
1.単元名 「1けたをかけるかけ算の筆算」 2.単元目標 算数への 関心・意欲・態度 とする。筆算や暗算の良さに気付く。 (2、3位数)×(1位数)の計算方法を考えよう 数学的な考え方 (何十・何百)×(1位数)の計算の仕方を、10(2)千の位に繰り上がるかけ算の筆算をする。 の筆算の仕方を理解する。 かけられる数が大きいときの筆算の仕方を考えよう (知・理、ノート・発言) る 部分積でもとめられた数はどの位なのか考えて (3位数)×(1位数) 筆算をする。実践記録算数4年 1.単元について 本単元では,初めて筆算形式によるわり算の仕方を学習する。 「立てる・かける・ひく・おろす」の手順でどんな数でも計算できるという筆算形式のよさに気づき,日常場面でも積極的に使っていこうとする意欲を
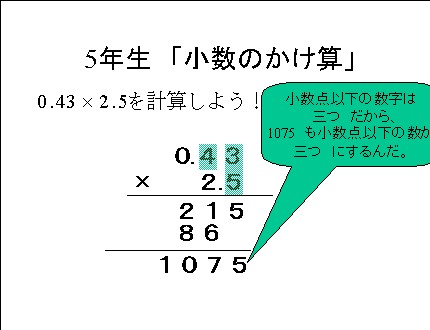
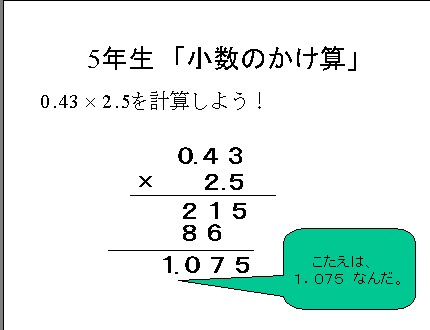
2 単元名 2位数×2位数のかけ算の筆算 3 単元の目標及び評価規準 (1) 目標 筆算による2位数に2位数をかける乗法計算の仕方について理解し、それを用いる能力を高め る。 (2) 評価規準本単元 かけ算の筆算(1) ・何十,何百×1 位数の計算 ・2,3 位数×1 位数の計算と 筆算形式 ・乗法の結合法則 ③ わり算の筆算 ・「商」「積」の用語 ・乗除の混合式の計算 ① かけ算 ・分配法則の活用 ・交換法則の活用 ・a× , ×a ⑭ かけ算の筆算(2)小数点の掛け算のやり方 次の計算をしましょう。 まずは、小数点を無視! を計算します。 すると、このような答えが求まります。 答えが求まったら、ここから小数点を動かしていきます。 これで計算は完成! やり方はシンプルでしたね。 それでは、いろんな問題を解きながら理解を深めていき
×3の筆算の仕方を考 える。 ・42×3、58×3の筆算 の仕方を考える。 ・筆算の仕方をまとめ る。 ★既習を生かして23 ×3の筆算の仕方を 考え、計算の過程を 説明できる。 5 2位数×1位数( 一の位の数との 部分積が2桁)の 筆算の仕方につ いて理解し、そ の計算 小数点は最後に調整するから、計算するときにはムシしててOKだよ! というわけで、小数点をなくして筆算の形にします。 こうなってくると、ただの掛け算と一緒だよね。 そして、筆算の答えが出たら最後に小数点の位置を調整します。 今回の計算では、小数点は合計で2個分あるって考えます。 なので、先ほど筆算でもとめた答えの2個分動かしたところに小数る ②2位数×1位 16×4の計算の仕方,筆算の仕方を考 部分積が2けたの場 数(部分積が える。 問題1 合も,同じように筆算 2けた)の筆 42×3,58×3の筆算の仕方を考える。 ができることを確かめ 算ができる。 問題2 ている。 5 ①2位数×1位 29×4の筆算の




小3 算数 小3 62 3けた 2けた 2けた Youtube




算数4年から6年
小数のかけ算 ~筆算の仕方~ 全員起立。 1.2×7.3を筆算の式で書きなさい。 書けたらすわりなさい。 子どもたちが書いているか確認する。 「前に書いたところと1行はあいているね。 あいてなかったら×をつけて書きなおしなさい。 」 と指示をする。・筆算の仕方を掲示する。(※4) ・加法の筆算の仕方を想起させ、繰り 上がった数を、十の位に小さく書か せる。(※5) ・繰り上がった数を、十の位に小さく 書いてあるか確認する。(※6) ・間違った筆算を示し、部分積を正し 1つ目は、筆算の手順を覚えることに つまずいていた子の事例です。 2ケタ×2ケタ となると、 かけ算をする順番や 答えをかく場所に 混乱してしまう子も出てきます。 このように、色分けされた形で 順番が示されていると、自分で確認しながら 筆算を



乗法の筆算とアルゴリズム 算数用語集




掛け算 筆算 を教える
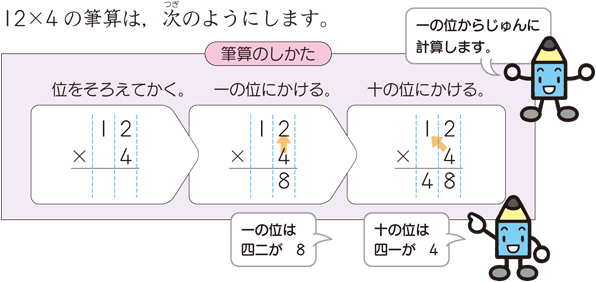
1 単元名 かけ算のしかたを考えよう 2 単元の目標 2~3位数×1位数の筆算の仕方について、乗法九九などの基本的な計算を基にできることのよ さに気づき、学習に生かそうとしている。 (関心・意欲・態筆算の仕方につ いて理解し、そ の計算ができ る。 算の仕方を考える。 ・筆算の仕方をまとめる。 2位数×1 位数(十の位 との部分積 が2桁、及び 部分積がみ な2桁)の筆 算ができる。 5 2位数×1位数 (部分積を加え たときに百の位 に繰り上がりあかけ算の筆算の大原則は 位ごとにかけて合わせる ことです。 次のように、かけ算した結果くり上がる場合も、同じタイルどうしを合わせます。そしてタイル10こで1本に、タイル10本で1枚にしてまとめていけばよいわけです。




3年算数 かけ算の筆算 2けた 2けた かけ算のくふう 実践報告 ネコ好きな学校の先生の日常



3年の かけ算の筆算 2 佐々木先生の話はグッド 横山験也のちょっと一休み
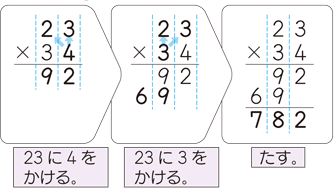
3年「2けたをかけるかけ算の筆算」 氏名 ★ (2けた)×(2けた)の筆算 3けた×2けたの筆算 チャレンジシート① 学ぶ かけ算の筆算は数字をたてにそろ えて,一の位からじゅんにかけてい くといいですね。 そうですね。一の位からじゅんに計算をし ます。⑵わり算の筆算のかき方の順序は, ③6,④は(̶)となる。わり算の筆 算は,たし算,ひき算,かけ算の筆算 とは形式が全く違い,演算記号の÷を 使わない。 2.ノートへのかき方の指導 筆算をノートにかくときは,問題の数字〈 計算の仕方 〉 ① かける数、かけられる数が整数 になるように、小数点を動かす。 ② 整数のかけ算の筆算をする。 ③ ①で動かした分だけもどす。 ( 小数点が先頭になったら0を 書 き足して、0を先頭




小学4年生の算数 小数のかけ算 筆算 十分の一までの小数 2桁までの整数 練習問題プリント ちびむすドリル 小学生
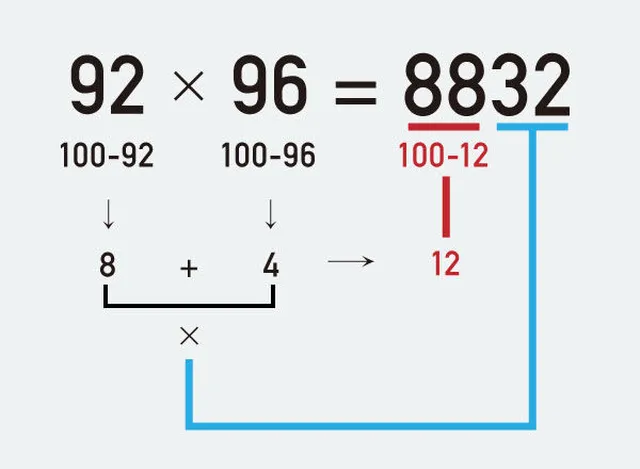



一瞬で解ける 最強 かけ算テク 4つ Tabi Labo
かけ算の筆算の仕方をたしかめ て、いろいろな問題をとこう。 力をつけるもんだいをしましょ う。 長いなわと短いなわがあります。 短いなわの長さは140cmです。 長いなわの長さは、短いなわの長さ の3倍です。長いなわの長さは何c mですか。実践記録算数3年 1.単元名 かけ算の筆算の仕方を考えよう「1けたをかけるかけ算の筆算」 2.指導によせて (1)指導内容 本単元において指導する内容は,2位数や3位数に1位数をかける乗法の計算に関わる内容である。 本単元では,これらの乗法の3 何十何×何の筆算のやりかたはどのようにすれ ・筆算は縦の式だ。 ・10と1に分けて計算する。 ・位を分けて計算する。 ・答えは一段にできるかな。 ・これまでのかけ算の計算を使って 筆算の計算の仕方を考えることが できる。 (考)〈発表・ノート〉




掛け算の筆算の計算手順 筆算の仕組みを子どもに教える方法を紹介 数学fun



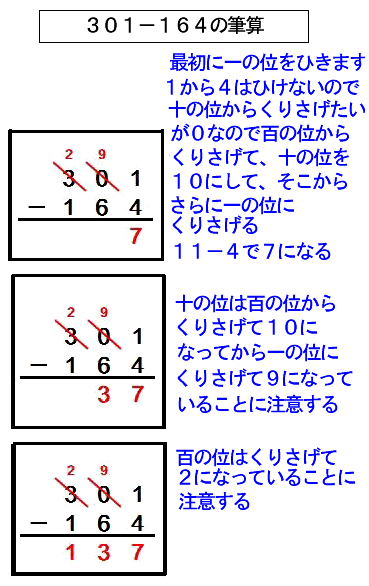
0 の沢山つくかけ算のひっ算は要注意
前時の内容と関連付けて,筆算の意味を考える。 本時の学びを単元テーマとともに振り返る。 2 位数×1 位数の筆算の仕方について理解している。評価1 ☆ 求答の手続き的な学びにならないよう,九九 での学びの想起を促し,かけ算の意味について下のような筆算の間違いに気づくことができると理解が深まり、計算違いが少なくなります。 つながる単元・・・3年「かけ算の筆算2」へ 最後に 3年生は、後半の教科書で、2けた×2けたのかけ算と3けた×2けたのかけ算を勉強します。ここでは、「かけ算の筆算」の学習のその発展として、 世界のいろいろなかけ算の方法を紹介した。 日本の筆算と「共通するところ」や「違うところ」を見つけていく中で、 かけ算の意味の理解を深めてほしいと考えたのである。 ・・・・・・・・・



1



三桁の掛け算の筆算のやり方を教えてください 3桁 3桁でしょうか 2桁 Yahoo 知恵袋
めあて3けたのかけ算の計 算の仕方を考え、せつ明しよう。 2 計算の仕方を考える。 ・図 ・位ごとの計算 ・筆算 137 +274 274 3 考えた結果を話し合い、学 習をまとめる。 まとめ3けたのかけ算の計 算も、2けたの計算と同じよう小学生のかけ算の問題プリントを作りました。 単元・内容ごとに順を追って、または、やりたい内容をピンポイントで選んで、くりかえし練習・学習ができるプリント集です。 小学2年生のかけ算九九 練習問題プリント 小学3年生のかけ算筆算



堺市立三国丘小学校 のホームページ



小数 小数のかけ算のやり方 大人の学び直し算数 計算のやり方解説 無料




世界中どこでも同じではなかった筆算 Everyday




算数4年から6年




夫婦 親子世代間で計算方法が変わったの 学習障害むすこ 空気は読むが字は読めない



0 の沢山つくかけ算のひっ算は要注意



乗法の筆算とアルゴリズム 算数用語集




小数点の掛け算 やり方は 筆算などの問題を解説 数スタ




掛け算 筆算 を教える




なぜかけ算の順序を決めて指導するのか Freedu



掛け算の筆算のやり方 大人の学び直し算数 計算のやり方解説 無料
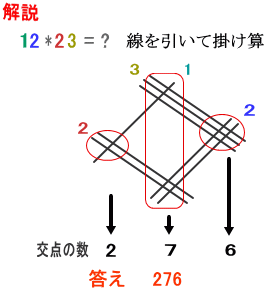



インド式掛け算 線を引いて 高精度計算サイト



Www Wakayama Wky Ed Jp Nagusa Wp Content Uploads Sites 52 18 03 D4eb1f5534f4dee52d11a190a01d 1 Pdf




2けた 1けたのかけ算の筆算 低学年の無料学習ドリル
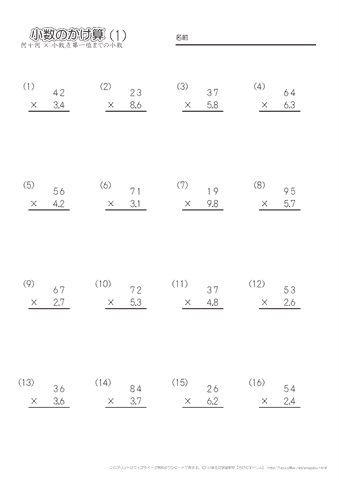



小数のかけ算 筆算 2桁の整数 十分の一までの小数 問題プリント ちびむすドリル 小学生




3年算数 かけ算の筆算 2 4時間目 2けた 2けたの計算の仕方と筆算の仕方を考えよう 例57 62 Youtube
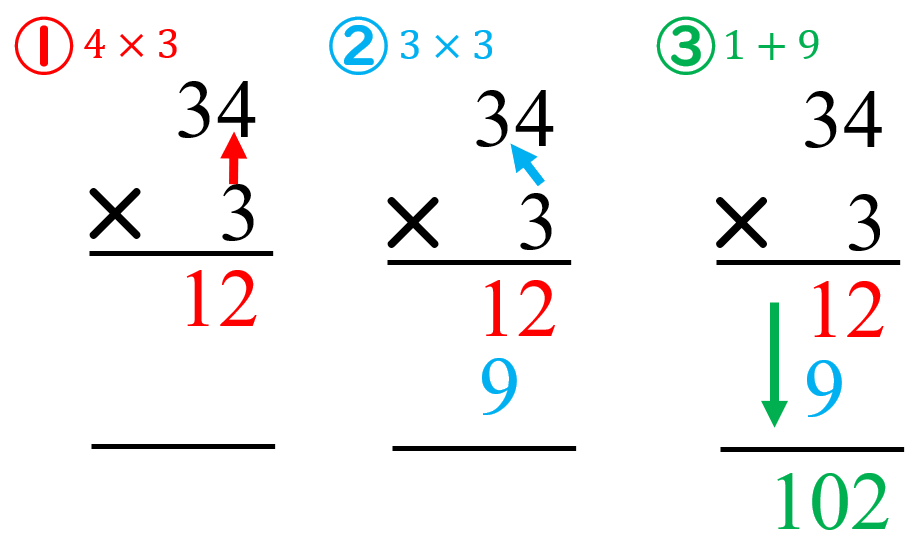



掛け算の筆算の計算手順 筆算の仕組みを子どもに教える方法を紹介 数学fun



3年算数 かけ算の筆算教え方
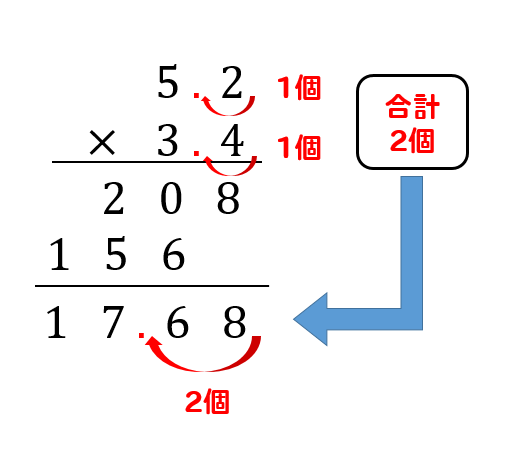



小数点の掛け算 やり方は 筆算などの問題を解説 数スタ
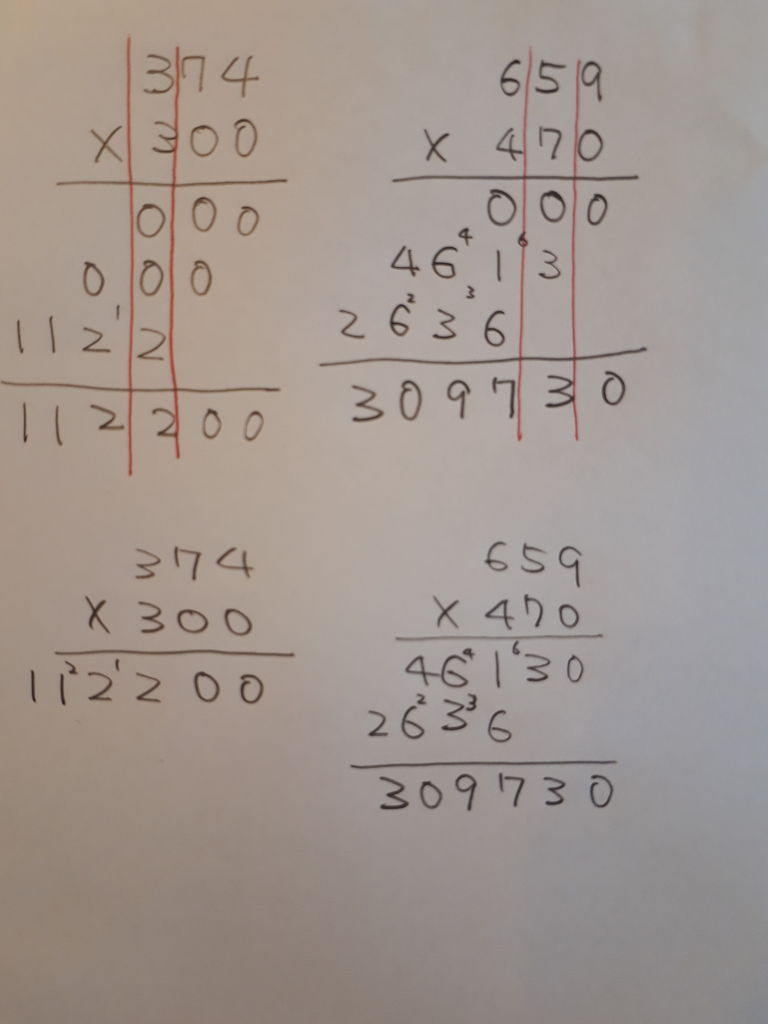



0 のある数字同士のかけ算は 意外と難しい 小 中学生向け補習塾 算数 数学 国語 ほめるん By じりつ堂




かけ算の筆算 2桁 1桁 算数無料問題 算数プリント
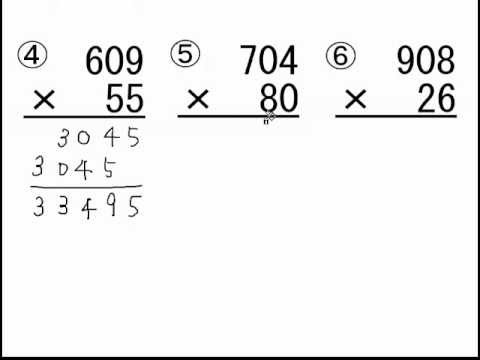



かけ算のひっさん 3けた 2けた Youtube
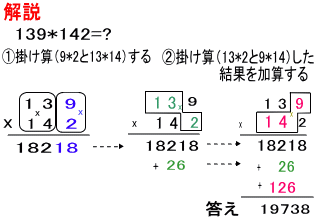



インド式掛け算 筆算 高精度計算サイト



パワーポイント教材 那須烏山市立烏山小学校
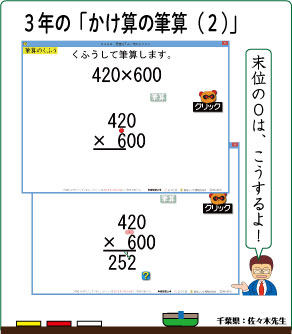



3年生の かけ算の筆算 2 のソフトを1本 開発中 さくら社




Asahi Com 朝日新聞社 外国のわり算に学ぶ 花まる先生公開授業 教育



Http Www Kochinet Ed Jp Shimizu E Kounaikensyuu Tangenkousouzu3nen Pdf



掛け算の筆算のやり方 大人の学び直し算数 計算のやり方解説 無料
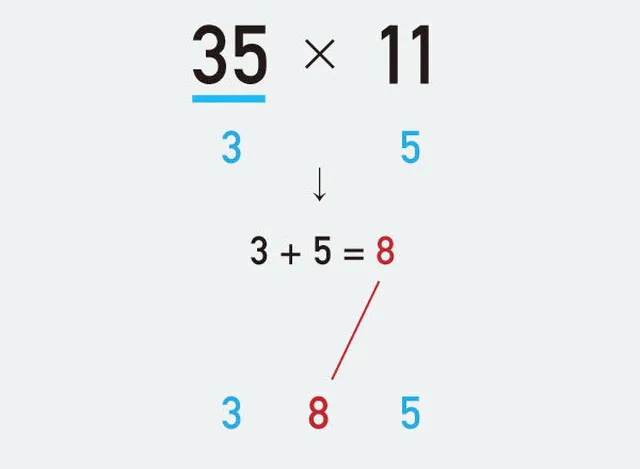



一瞬で解ける 最強 かけ算テク 4つ Tabi Labo




足し算の筆算の計算手順 筆算の仕組みを子どもに教える画期的な方法を紹介 数学fun
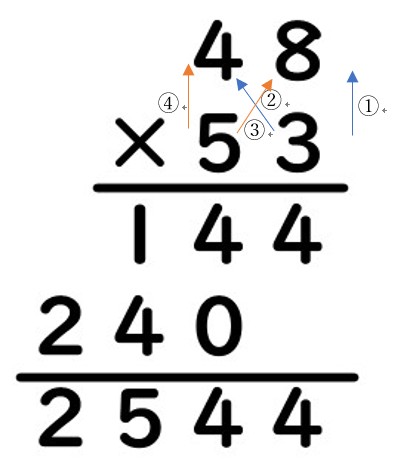



本日の授業 4年生算数 大きな数のかけ算 筆算の仕組み わかっているかな 現役小学校教員による授業実践 学級経営記録
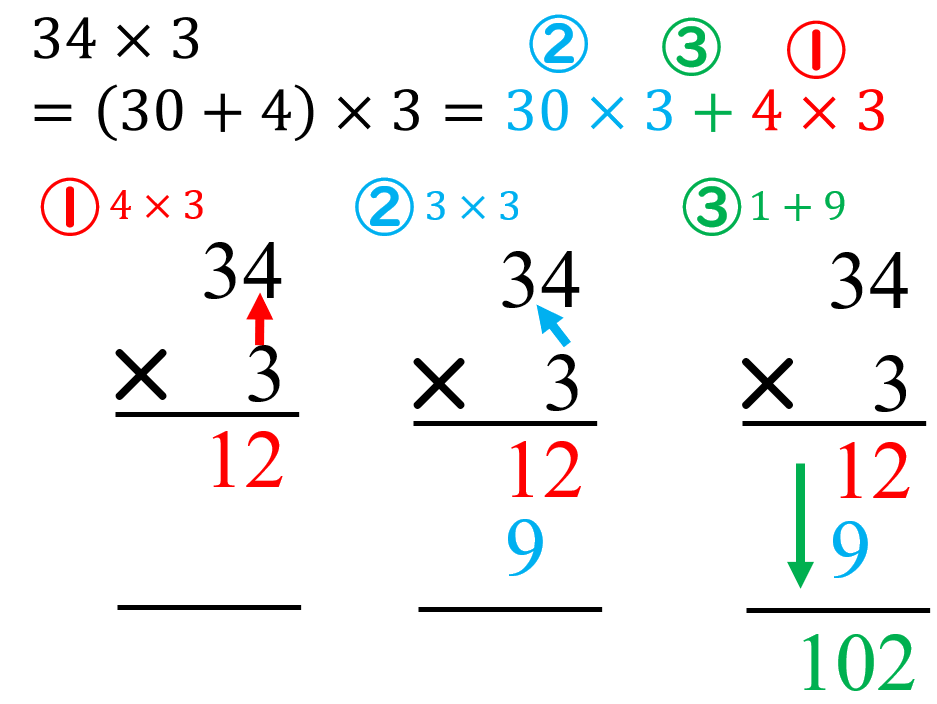



掛け算の筆算の計算手順 筆算の仕組みを子どもに教える方法を紹介 数学fun



3年算数 かけ算の筆算教え方
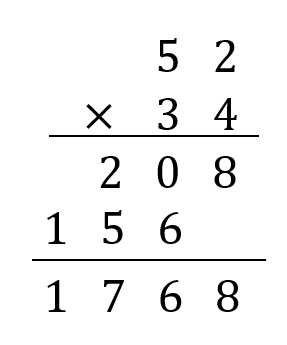



小数点の掛け算 やり方は 筆算などの問題を解説 数スタ
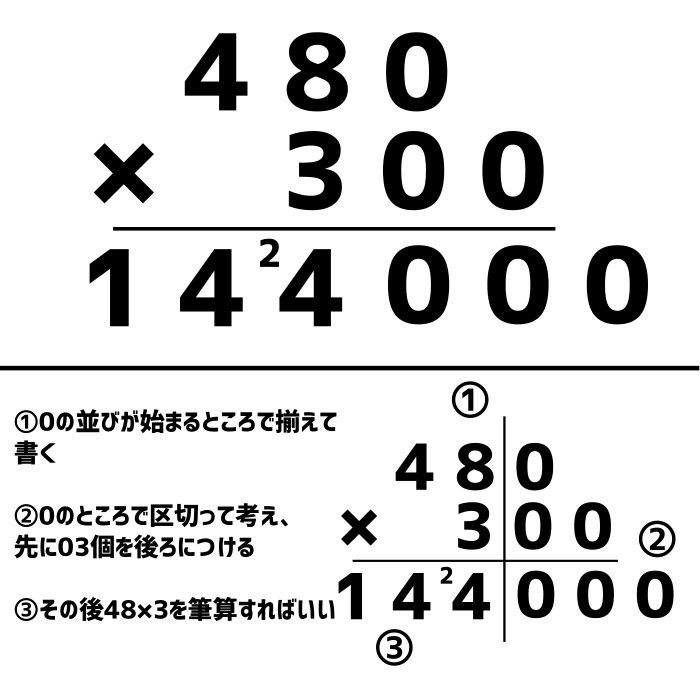



かけ算の筆算で使えるテクニック チーム エン




12 小学2 3年生の算数 大きい数の掛け算 掛け算の筆算のやり方はくり上がりに気を付けよう 無料学習 掛け算3時間目 キッキブログ なんで を探す




2けたのかけ算 筆算 練習 Youtube



パワーポイント教材 那須烏山市立烏山小学校
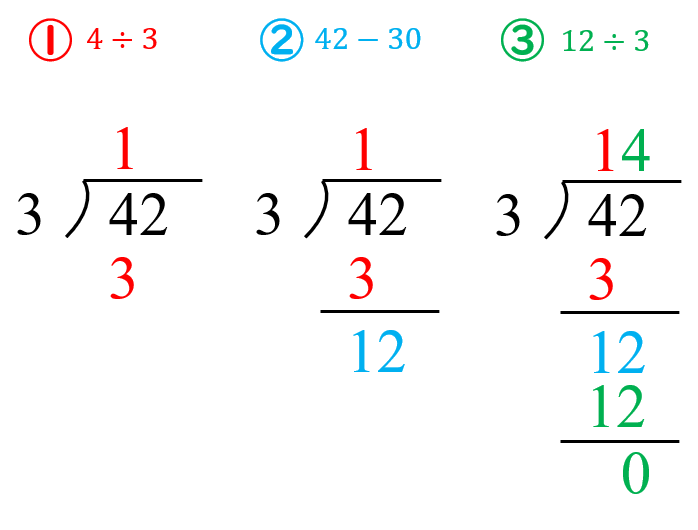



割り算の筆算の計算手順 筆算の仕組みを子どもに教える方法を紹介 数学fun




夫婦 親子世代間で計算方法が変わったの 学習障害むすこ 空気は読むが字は読めない



掛け算の筆算のやり方 大人の学び直し算数 計算のやり方解説 無料




小数のかけ算 小学4 5年生算数 無料学習プリント




小学3年生の算数 筆算 掛け算 3桁 1桁 4桁 練習問題プリント ちびむすドリル 小学生




掛け算 筆算 を教える




小数点同士の掛け算 やり方




小学4年生 算数 無料問題集 4桁 2桁の掛け算の筆算 おかわりドリル



掛け算の筆算のやり方 大人の学び直し算数 計算のやり方解説 無料



2けたをかける かけ算の筆算 港区立青山小学校 算数3年生の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材




世界の算数 数学やりかた色々 筆算は各国こんなにも違う



3年算数 かけ算の筆算教え方




小数の割り算の筆算 教え方 やり方 なぜ小数を動かすのか 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の小学生専門 国語と算数の苦手を克服



筆算をする電卓




すきるまドリル 小学3年生 算数 かけ算の筆算 1 無料学習プリント すきるまドリル 無料学習プリント




3けた 3けたの筆算 小学生無料算数学習プリント 無料プリントのぷりんと365



かけ算の筆算 Multiplication を動画でマスター インド式もあり 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材



1




かけ算の筆算 3けた 1けた Youtube




小数のかけ算が苦手 を克服する方法 中学受験ナビ




掛け算の筆算の 本質部分 を図解により説明します 算数 数学 の文章題 特殊算など のことを書くページ
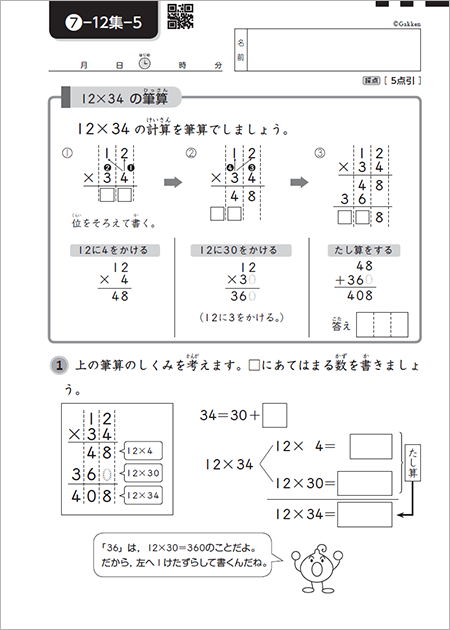



学研教室




12 小学2 3年生の算数 大きい数の掛け算 掛け算の筆算のやり方はくり上がりに気を付けよう 無料学習 掛け算3時間目 キッキブログ なんで を探す
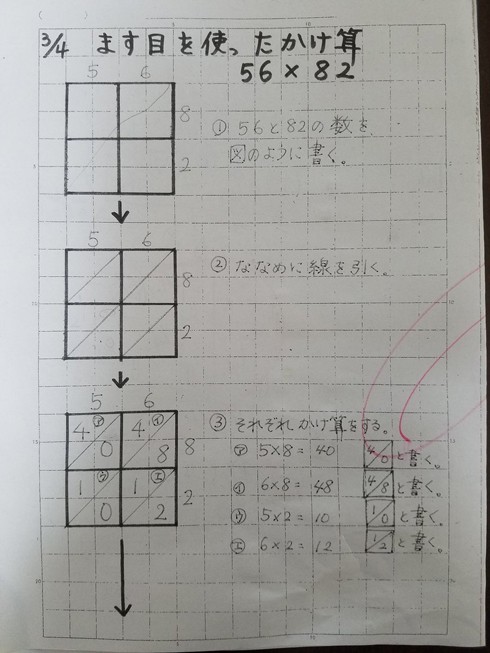



何その計算方法 ノートのマス目を九九で埋めて足し算するだけ の筆算でケアレスミスが減らせるかも ねとらぼ
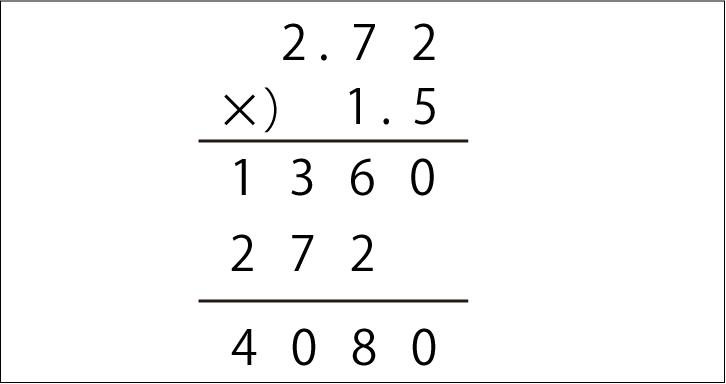



小数のかけ算が苦手 を克服する方法 中学受験ナビ
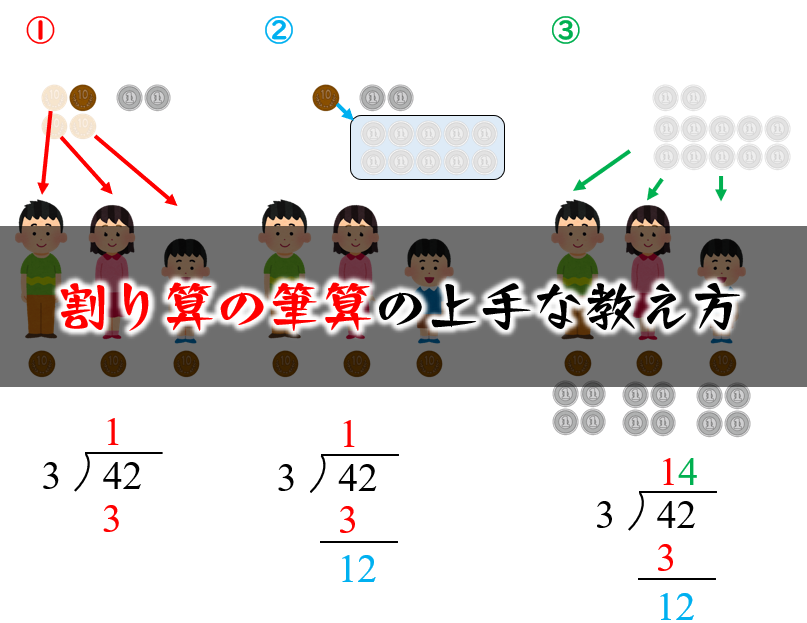



割り算の筆算の計算手順 筆算の仕組みを子どもに教える方法を紹介 数学fun




小数点の掛け算 やり方は 筆算などの問題を解説 数スタ
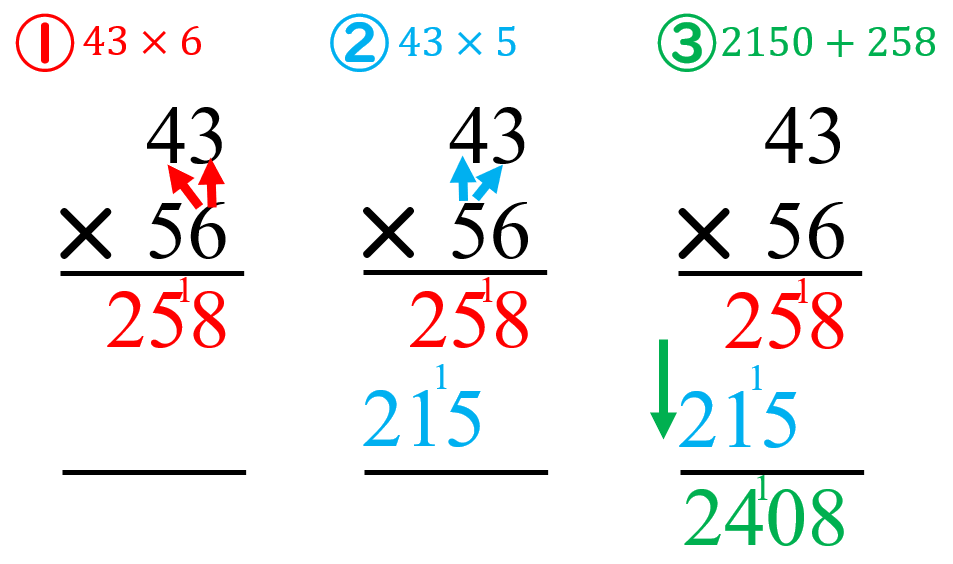



掛け算の筆算の計算手順 筆算の仕組みを子どもに教える方法を紹介 数学fun




3年算数 かけ算の筆算 2けた 2けた かけ算のくふう 実践報告 ネコ好きな学校の先生の日常



かけ算 掛け算 の教え方は水道方式でわかりやすく 数学で育ちあう会



かけ算のひっさん 3けた 3けた 問題練習 Youtube



前田の算数 インド式かけ算



小学3年生の算数 の教え方の例 算数数学が苦手な子専門のプロ家庭教師みかん先生




かけ算のひっさん 2けた 2けた 問題練習 Youtube



インド式2桁 2桁の掛け算



4年算数小数 整数 小数 整数 1 教え方



3年生算数たし算とひき算の筆算 2 わかる教え方




小学3年生の算数 筆算 掛け算 2桁 2桁の計算 練習問題プリント ちびむすドリル 小学生




掛け算の筆算の計算手順 筆算の仕組みを子どもに教える方法を紹介 数学fun



3



算数4年から6年



掛け算の筆算のやり方 大人の学び直し算数 計算のやり方解説 無料
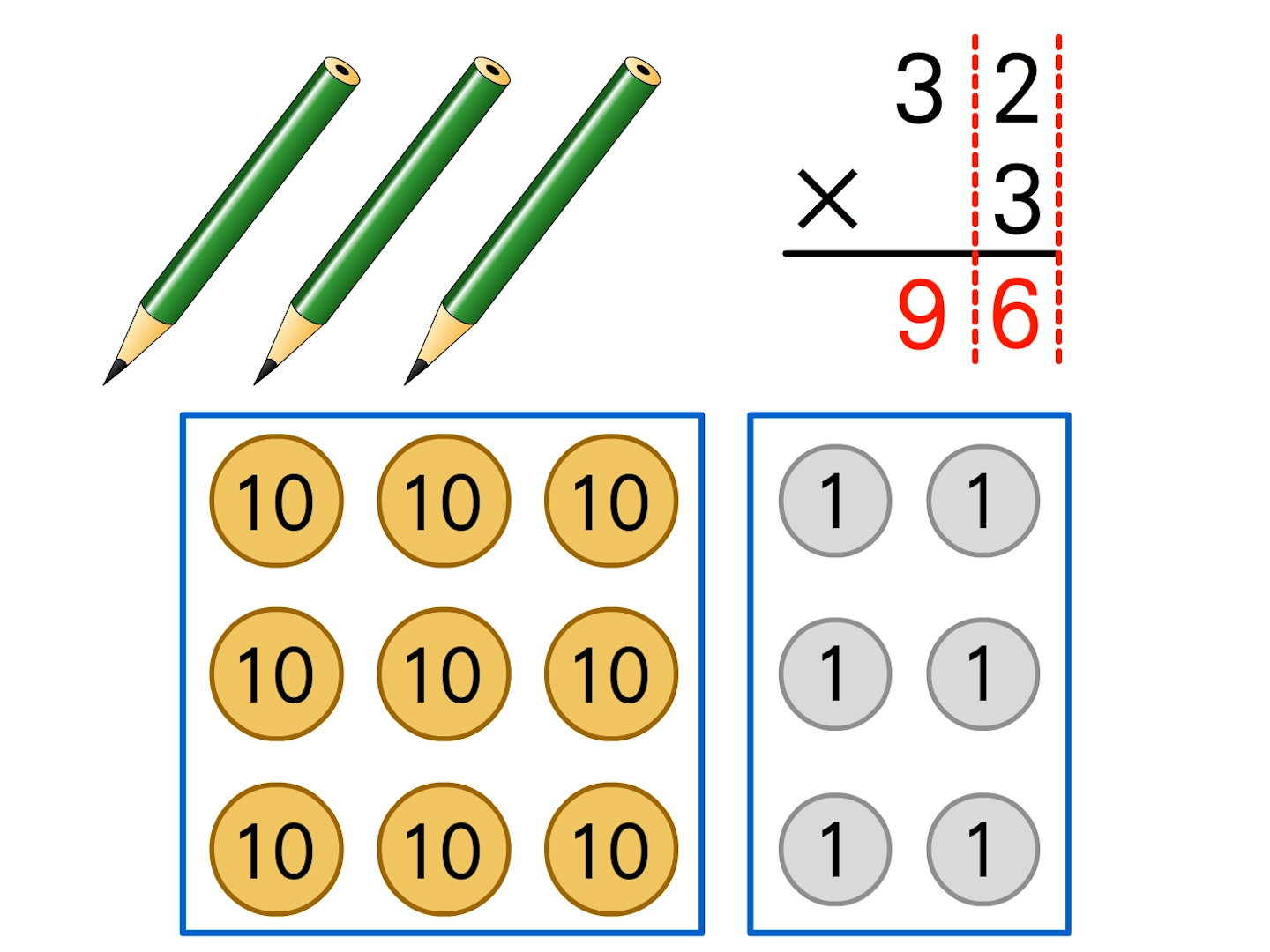



3年 かけ算の筆算 算数イメージ動画集 大日本図書



掛け算の筆算のやり方 大人の学び直し算数 計算のやり方解説 無料



3年算数 かけ算の筆算教え方



2けたをかける かけ算の筆算 港区立青山小学校 算数3年生の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材



かけ算 掛け算 の教え方は水道方式でわかりやすく 数学で育ちあう会




小4 小数の割り算の筆算のやり方は あまりと答えの小数点は位置が違う 小5 そうちゃ式 分かりやすい図解算数 割り算 算数 特別支援教育




計算 かけ算の筆算 2桁 2桁 01 10 プリントok



1




本日の授業 4年生算数 大きな数のかけ算 筆算の仕組み わかっているかな 現役小学校教員による授業実践 学級経営記録




掛け算の筆算 フツウじゃないよ でもダイジョウブ




かけ算のひっさん 3けた 1けた Youtube
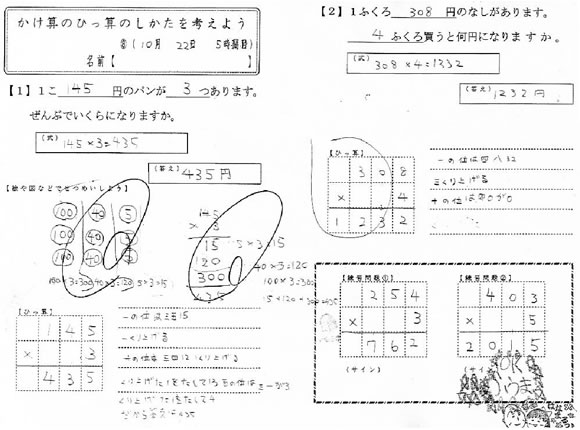



実践記録算数3年



0 件のコメント:
コメントを投稿