Cross multiplication is only applicable when we have a pair of linear equations in two variables Let us suppose that a1x b1y c1 = 0 and a2x b2x c2 = 0 are the two equations which has to be solved By using cross multiplication, we will get the values x and y such as x = b1 c2 − b2 c1 b2 a1 − b1 a2 x = b 1 c 2 − b 2 c 1 b 2 a 1 Ex 21, 1 If (x/3 " 1, y –" 2/3) = (5/3 "," 1/3) , find the values of x and y (x/3 " 1, y –" 2/3) = (5/3 "," 1/3) Since the ordered pairs are equal, corresponding elements are equal Hence x/3 1 = 5/3 x/3 = 5/3 – 1 x/3 = 2/3 x = 2 y – 2/3 = 1/3Subtract x^ {3} from both sides Subtract x 3 from both sides Combine x^ {3} and x^ {3} to get 0 Combine x 3 and − x 3 to get 0 Reorder the terms Reorder the terms This is true for any x This is true for any x Use the distributive property to multiply xy by x^
Solve Each Of The Following Systems Of Equations By The Method Of Cross Multiplication X 2y 1 0 2x 3y 12 0 Sarthaks Econnect Largest Online Education Community
2/x-1 3/y 1=2 3/x-1 2/y 1=13/6 by cross multiplication
2/x-1 3/y 1=2 3/x-1 2/y 1=13/6 by cross multiplication-= (3/2)(1/2) (3/2)(1/2) (3/2)(1/2) = 9/4 Problem 8 For this problem, please consider three linear and timeinvariant channels, channel one, channel two, and channel three The unit sample response for each of these three channels are plotted below Please use these plots to answer all the parts of this question ASimple and best practice solution for y=1/2x1;y=3/2x3 Check how easy it is, to solve this system of equations and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework




Solve The Equations 5x 1 1y 2 2 And 6x 1 3y 2 1
Question Solve for y y 1/2 = 1/3 (x 1/2) What I have done y 1/2 = 1/3x 1/2 * 1/3 y 1/2 = 1/3x 2/6 (THIS SHOULD BE 1/6) y 1/2 1/2 = 1/3 x 2/6 1/2 y = 1/3x 10/12 y = 1/3x 5/6 y = 1/3x / 1/3 5/6 / 1/3 y = x 15/6 FoundAn example in three variables is x³ 2xyz² − yz 1 Square Root In mathematics, a square root of a number x is a number y such that y² = x;X^2y^2=1, (x2)^2(y1)^2=4 Natural Language;
Graph y=2(x1)^23 Find the properties of the given parabola Tap for more steps Use the vertex form, , to determine the values of , , and Since the value of is negative, the parabola opens down Opens Down Find the vertex Find , the distance from the vertex to the focus Transcript Example 17 Solve the pair of equations 2/𝑥 3/𝑦=13 5/𝑥−4/𝑦=−2 2/𝑥 3/𝑦=13 5/𝑥−4/𝑦=−2 So, our equations become 2u 3v = 13 5u – 4v = –2 Hence, our equations are 2u 3v = 13 (3) 5u – 4v = – 2 (4) From (3) 2u 3v = 13 2u = 13 – 3V u = (13 − 3𝑣)/2 Putting value of u (4) 5u – 4v = 2 5((13 − 3𝑣)/2)−4𝑣=−2 MultiplyingA = 22/(11) = 2, b = 33/(11) = 3 x = 1/2, y = 1/3 Hence the solution is (1/2, 1/3) Question 2 Akshaya has 2 rupee coins and 5 rupee coins in her purse If in all she has 80 coins totalling ₹ 2, how many coins of each kind does she have Solution Let "x" and "y" number of 2 rupee and 5 rupee coins respectively
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historySolve the Following Simultaneous Equations 2 X 3 Y = 13 ; Ex 35, 1 Which of the following pairs of linear equations has unique solution, no solution, or infinitely many solutions In case there is a unique solution, find it by using cross multiplication method x – 3y – 3 = 0 3x – 9y – 2 = 0 x – 3y – 3 = 0 3x – 9y – 2 = 0 x – 3y –




Cross Multiplication Method For Solving Equations A Plus Topper




Daily Food Consumption Of Selected Food Groups According To Children In Download Table
Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorSimple and best practice solution for 2(x1)3=x3(x1) equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itSimple and best practice solution for y3=2(x1) equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework 2x2=8 x3=5 3x2=18 2x10=12 6x2=14 3x=12 4x2=12 9x3=6 12x=5 x8=13 all equations



Solve The System Of Equations By Using The Method Of Cross Multiplication 1 X 1 Y 7 2 X 3 Y 17 Sarthaks Econnect Largest Online Education Community




1 2x 1 3y 2 1 3x 1 2y 13 6 Xand Y Is Not 0 Brainly In
Solution for 3 3 2 X 2 1 1 2 3 3 2 1 1 2 3 3 2 2 3 y = f(x) = x 1 (i) (ii) 3 3 2 2 1 x x x 3 211 i 2 3 321, 1 2 3 32 2 2From the equation 3(x1)^2 3(y1)^2 = 6 we divide everything by 3 and get (x1)^2 (y1)^2 = 2 This is the equation of a circle with center at (Chapter 1 Rational and Irrational Numbers Chapter 2 Compound Interest (Without using formula) Chapter 3 Compound Interest (Using Formula) Chapter 4 Expansions (Including Substitution) Chapter 5 Factorisation Chapter 6 Simultaneous (Linear) Equations (Including Problems) Chapter 7 Indices (Exponents) Chapter 8 Logarithms Chapter 9 Triangles Congruency in Triangles




Ex 3 6 1 V And Vi 7x 2y Xy 5 8x 7y Xy 15



2
Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries Students (upto class 102) preparing for All Government Exams, CBSE Board Exam, ICSE Board Exam, State Board Exam, JEE (MainsAdvance) and NEET can ask questions from any subject and get quick answers bySolve the given inequalities 3x y ≥ 12, x y ≥ 9, x ≥ 0, y ≥ 0graphically in two – dimensional plane asked Jul 22 in Linear Equations by KumarArun (5 X − 4 Y = − 2 Maharashtra State Board SSC (English Medium) 9th Standard Textbook Solutions 4940 Important Solutions 3 Question Bank Solutions 2403 Concept Notes & Videos 2 Syllabus Advertisement Remove



2




Population Description Download Table
Steps for Solving Linear Equation y=2x1 y = 2 x − 1 Swap sides so that all variable terms are on the left hand side Swap sides so that all variable terms are on the left hand side 2x1=y 2 x − 1 = y Add 1 to both sides Add 1 to both sidesSelect a few x x values, and plug them into the equation to find the corresponding y y values The x x values should be selected around the vertex Tap for more steps Replace the variable x x with 2 2 in the expression f ( 2) = 2 ( 2) 2 − 12 ⋅ 2 19 f ( 2) = 2 ( 2) 2 12 ⋅ 2 19 Simplify the result Yuichiro13 Ace 552 answers 3336K people helped Heya Multiplying both sides by xy, we get Now, multiplying the first equation by (2) and subtracting from the second one, we get Hence, substituting the value in either equation and solving for y, we get Hence, we get ( x , y ) = ( 1 , 3 ) as the solution



Orcity Org




5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Solve The Following Pairs Of Equations By Reducing Them To Pair Of Linea Youtube
Simple and best practice solution for 1/3(x2)=2/3x13/3 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homeworkIn other words, a number y whose square (the result of multiplying the number by itself, or y ⋅ y) is x For example, 4 and −4 are square roots of 16, because 4² = (−4)² = 16X^2(y(x^2)^(1/3))^2 = 1 Natural Language;




Mathematics Sample Questions




Effect Of Temperature On Tribological Performance Of Organic Friction Modifier And Anti Wear Additive Insights From Friction Surface Tof Sims And Edx And Wear Analysis Sciencedirect
Let The new equation come General form of cross multiplication method is Put b's value in equation (5) Check from Equation (3) and (4) a which is used in place of u and b which is used in place of v Now finding u and v value Solve(cross multiplication method) 2/x3/y=2 1/x1/2y=1/3 Share with your friends Share 16 Dear student T a k i n g 1 x = u a n d 1 y = vCancel the common factor Divide ( x − 3) ( x 1) ( x 3) ( x 1) by 1 1 Divide 0 0 by 2 2 If any individual factor on the left side of the equation is equal to 0 0, the entire expression will be equal to 0 0 Set the first factor equal to 0 0 and solve
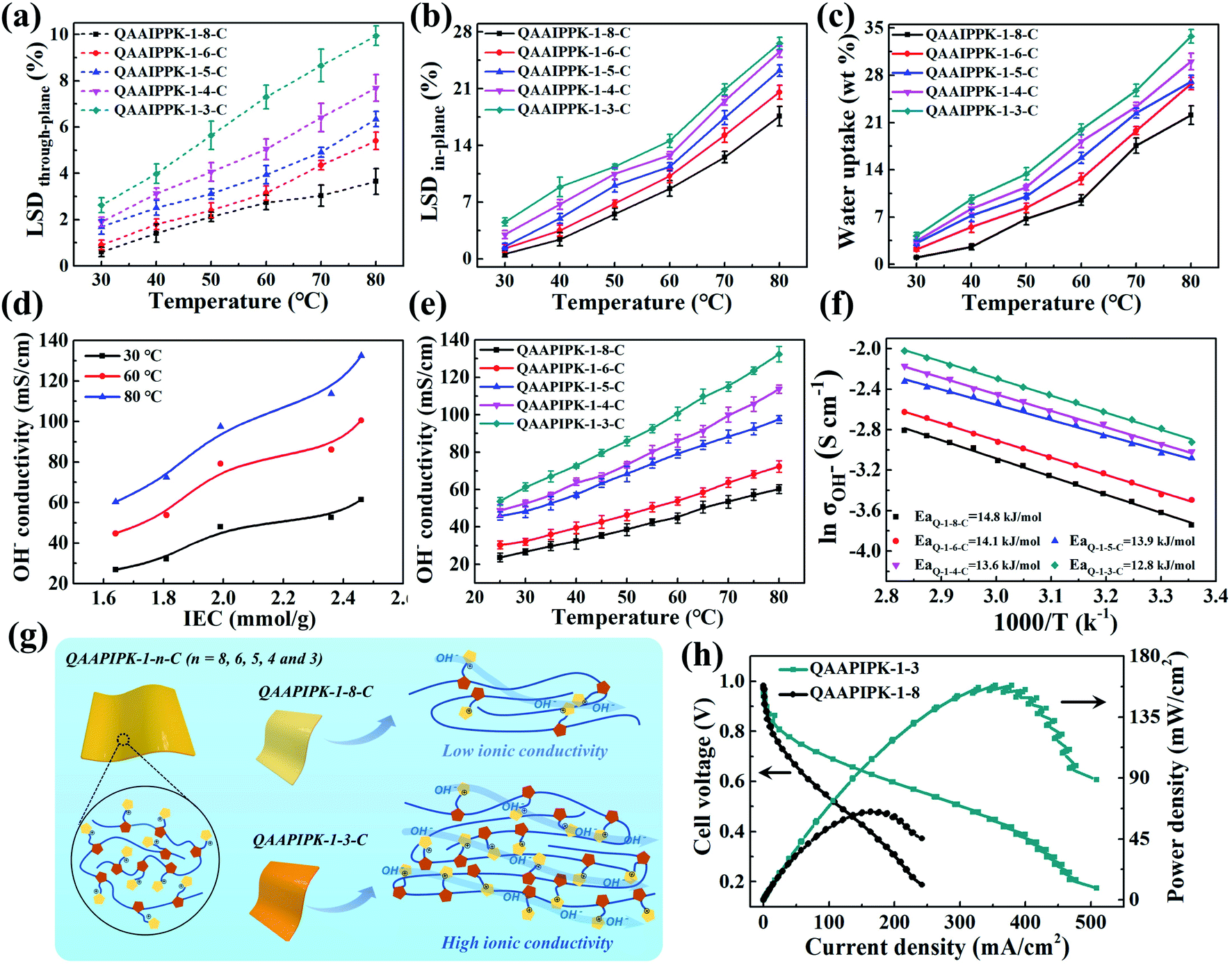



Imidazole Functionalized Polyketone Based Polyelectrolytes With Efficient Ionic Channels And Superwettability For Alkaline Polyelectrolyte Fuel Cells And Multiple Liquid Purification Journal Of Materials Chemistry A Rsc Publishing




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3
Transcript Ex 36, 1 Solve the following pairs of equations by reducing them to a pair of linear equations (i) 1/2𝑥 1/3𝑦 = 2 1/3𝑥 1/2𝑦 = 13/6 1/2𝑥 1/3𝑦 = 2 1/3𝑥 1/2𝑦 = 13/6 Let 1/𝑥 = u 1/𝑦 = v So, our equations become 1/2 u 1/3 v = 2 (3𝑢 2𝑣)/(2 × 3) = 2 3u 2v = 12 1/3 u 1/2 v = 13/6 (2𝑢 3𝑣)/(2 × 3) = 13/6 2u 3v = 13 Our equations Section 43 Double Integrals over General Regions In the previous section we looked at double integrals over rectangular regions The problem with this is that most of the regions are not rectangular so we need to now look at the following double integral, ∬ D f (x,y) dA ∬ D f ( x, y) d A where D D is any regionMath Input NEW Use textbook math notation to enter your math Try it




4 3 3 Matrices And Determinants



2
Transcript Example 18 Solve the following pair of equations by reducing them to a pair of linear equations 5/(𝑥 −1) 1/(𝑦 −2) = 2 6/(𝑥 −1) – 3/(𝑦 −2) = 1 5/(𝑥 − 1) 1/(𝑦 − 2) = 2 6/(𝑥 − 1) – 3/(𝑦 − 2) = 1 So, our equations become 5u v = 2 6u – 3v = 1 Thus, our equations are 5u v = 2 (3) 6u – 3v = 1 (4) From (3) 5u v = 2 v = 2Answer (1 of 2) 3/x2/y=0 take lcm or multiply both lhs and rhs with xy 3y2x=0 3y=2x substitute 3y=2x in the other equation 2/x2/(2x)=1/6 2/x1/x=1/6 as they are like fractions we can perform subtraction 1/x=1/6 therefore x=6 and substituting x=6 in any eqn find the value of yYou can put this solution on YOUR website!




1 2x 1 3y 2 1 3x 1 2y 13 6 Solve The Pair Of Equations By Reducing Them To A Pair Of Linear Equation Youtube



C1
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreSimplify\\frac{x^214x49}{49x^2} simplify\\frac{6}{x1}\frac{3}{x1} simplify\\frac{5x}{6}\frac{3x}{2} simplifycalculator en Related Symbolab blog posts Middle School Math Solutions – Equation Calculator Welcome to our new "Getting Started" math solutions series Over the next few weeks, we'll be showing how SymbolabSOLUTION V(3X 2Y) = 32V(X) 22V(Y) = 13




Amazon Com Mindware Subtraction Secrets Evelyn Christensen Toys Games




Solve The Equations 5x 1 1y 2 2 And 6x 1 3y 2 1
(x^21)^3=x^63x^43x^21 (ab)^3=a^33a^2b3ab^2b^3 (x^21)^3=(x^2)^33(x^2)^23x^21=x^63x^43x^21 How do you find the volume of a prism if the width is x, height is #2x1# and the length if #3x4#?Algebra Graph y=1/3x3 y = − 1 3 x 3 y = 1 3 x 3 Rewrite in slopeintercept form Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m x b Write in y = m x b y = m x b form Tap for more stepsExamples on Cross Multiplication Method Example 1 Help Fredie to solve the following pair of linear equations by crossmultiplication 2x5y−52 = 0 3x−4y14 = 0 2 x 5 y − 52 = 0 3 x − 4 y 14 = 0 Solution The terms below x, negative y, and 1 are calculated below Thus, the solution is



1 2x 1 3y 2 1 3x 1 2y 13 6




1 2x 1 3y 2 1 3x 1 2y 13 6 Solve The Pair Of Equations By Reducing Them To A Pair Youtube
Graph{x^33x^29x5 1459, 1726, 856, 736} FIrst determine the interval of definition, then the behavior of first and second derivatives and the behavior of the function as \displaystyle{x}Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music1/3 * (1/2 3 3/8) The calculator performs basic and advanced operations with fractions, expressions with fractions combined with integers, decimals, and mixed numbers It also shows detailed stepbystep information about the fraction calculation procedure Solve problems with two, three, or more fractions and numbers in one expression
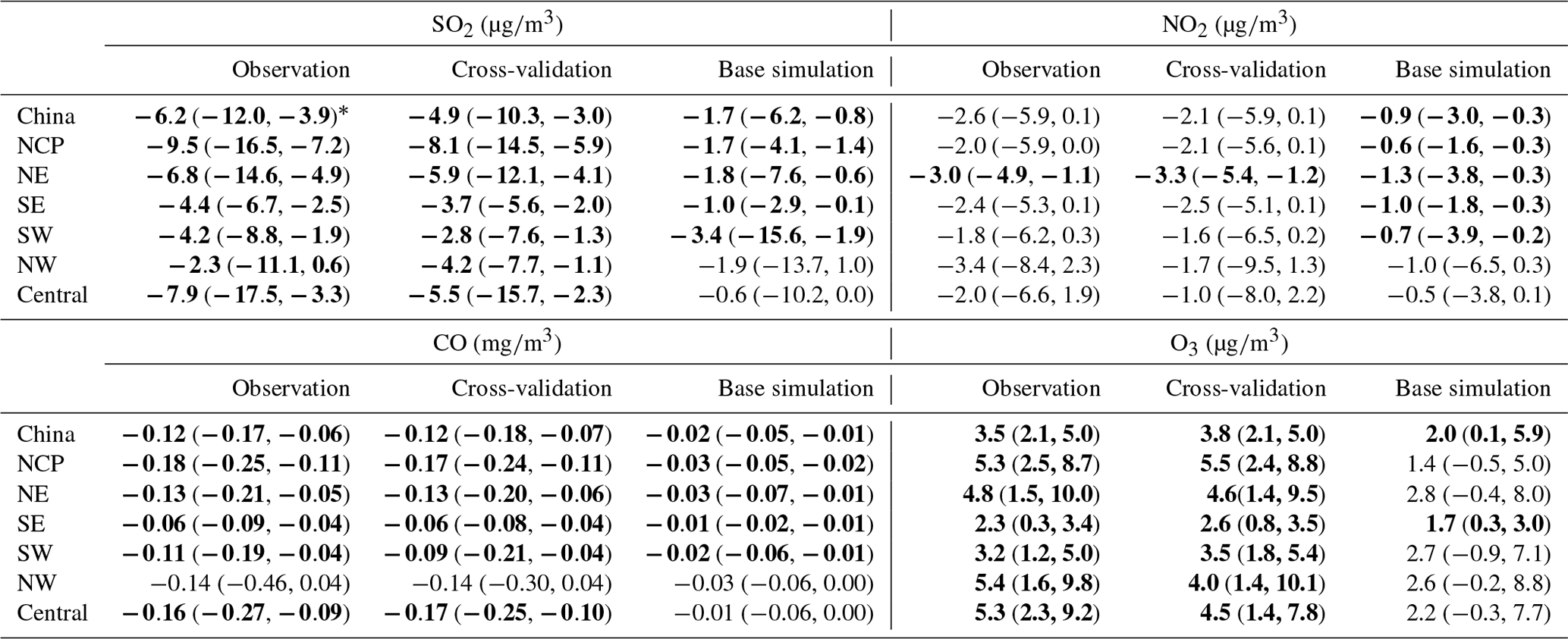



Essd A 6 Year Long 13 18 High Resolution Air Quality Reanalysis Dataset In China Based On The Assimilation Of Surface Observations From Cnemc




Molecular Engineering Of Microporous Crystals Ii A New Method To Describe The Structures Of Zeolites And Related Open Framework Crystalline Materials Sciencedirect
EXERCISE 36 CLASS 10 MATHS CHAPTER 3LINEAR EQUATIONS IN TWO VARIABLES NCERT Solutions For Class 10 Maths Chapter 3 Linear Equations In Two Variables Ex 36 given here are prepared by the subject experts Visit now to download solutions in PDF for freeMath Input NEW Use textbook math notation to enter your math Try it1 −2 −1 3 x y Change of coordinates in Rn The usual (standard) coordinates of a vector • Cross product with a fixed vector L R3 → R3, L(v) = v×v0, where v0 ∈ R3 • Multiplication by a fixed matrix L Rn → Rm, L(v) = Av, where A is an m×n matrix and all vectors are column vectors




Solve 5 X 1 2 Y 1 1 2 10 X 1 2 Y 1 5 2 Brainly In




Algebra 2 Solutions Pdf Integer Rational Number
Let y= 0 and solve for x 2(x1)^23 = 0 (x1)^2 = 3/2 Since the square equals a negative value x1 is a complex number (not a Real Number) So the xintercepts are complex The graph of your function does not cross the xaxis There are no xintercepts Cheers,Gives the answers for (a)(c) as E(XY) = 3 2, E(XY) = 1 2, and E(X Y)2 = E(X2) 2EXEY E(Y2) = 4 3 For part (d) we must also compute E(e2Y) = Z 1 0 e2ye ydy= Z 1 0 eydy= 1 Therefore, E(X2e2Y) = 1 Problem 7 (p 367 #6) Let Xand Y be independent standard normal variables Find 3 a) P(3X 2Y >5);A L(x 1,x 2,x 3) b L(1,0,0),L(0,1,0),L(0,0,1) L(x 1,x 2,x 3) = 1 −1 2 4 1 3 x 1 x 2 x 3 = x 1 −x 2 2x 3 4x 1 x 2 3x 3 L(1,0,0) = (1,4)T L(0,1,0) = (−1,1)T L(0,0,1) = (2,3)T The reader should note that L(e 1) is the first column of A, L(e 2) is the second column of A, and L(e 3) is the third column In general, if Ais an m× nmatrix




2 X 1 3 Y 1 2 3 X 1 2 Y 1 13 6 Find X And Y Brainly In




Solve For X And Y X 1 2 Y 1 3 9 And X 1 3 Y 1 2 8 Brainly In
Simple and best practice solution for 3/x11/2=1/3x3 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homeworkExtended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music




Solve The Following Pairs By Reducing Them To A Pair Of Linear Equation 1 2x 1 3y 21 3x 1 2y Brainly In



Radical Functions And Rational Exponents Pages 372 Manualzz
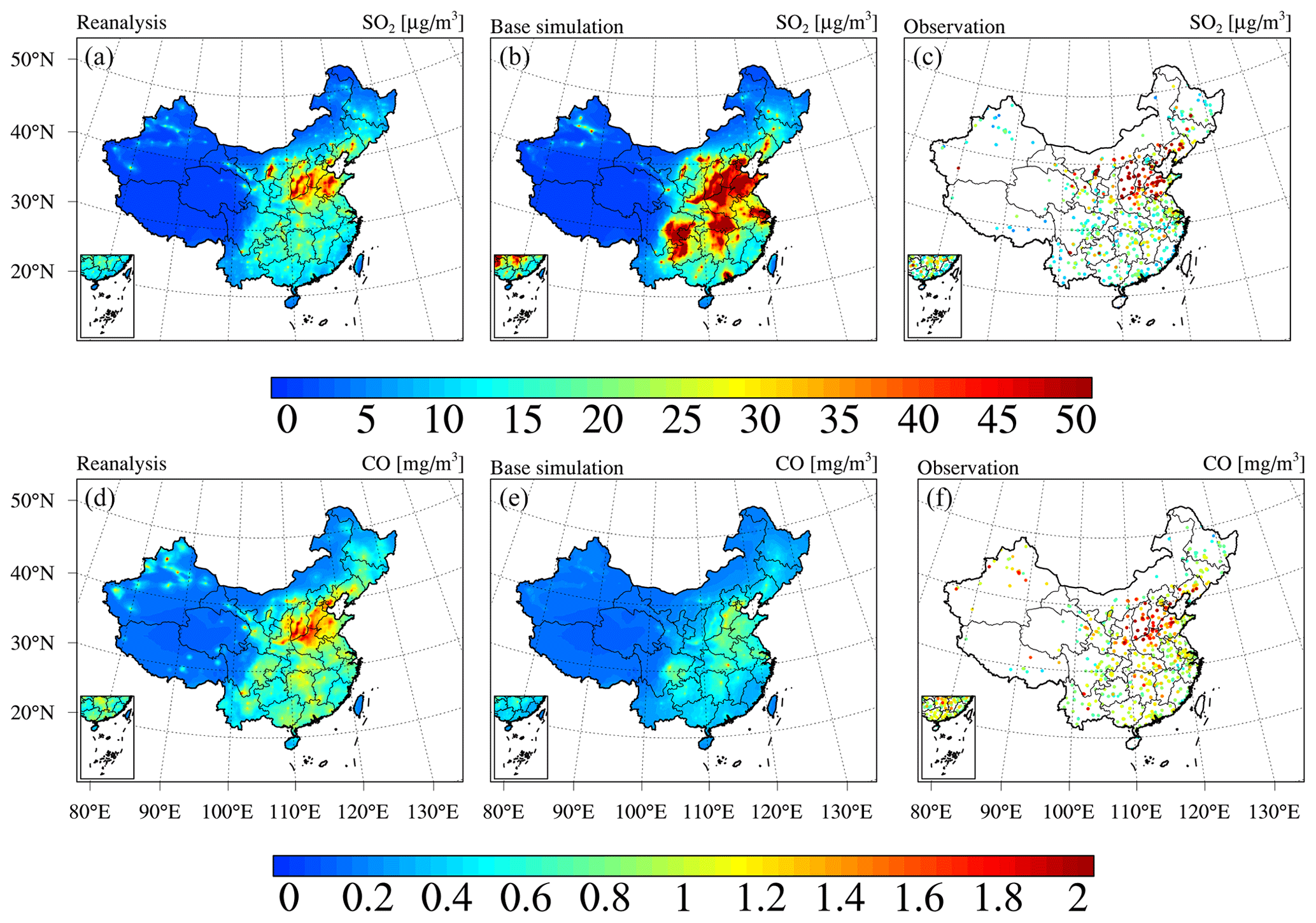



Essd A 6 Year Long 13 18 High Resolution Air Quality Reanalysis Dataset In China Based On The Assimilation Of Surface Observations From Cnemc
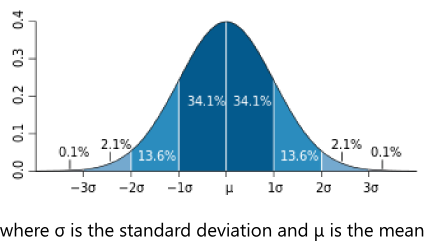



Biostatistics




Solving Linear Equations By Cross Multiplication Method X 2y 2 X 3y 7 Brainly In



Solve The System Of Equations By Using The Method Of Cross Multiplication 3x 2y 3 0 4x 3y 47 0 Sarthaks Econnect Largest Online Education Community




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y




Kindly Solve 2x Y 5 And 3x 2y 8 Using Cross Multiplication Method Maths Pair Of Linear Equations In Two Variables Meritnation Com




Solve The Pair Of Linear Equations By Cross Multiplication Method 2 2x Y 5 3 X 3y 1 0 Brainly In



Solve The System Of Equations By Using The Method Of Cross Multiplication X 6 Y 15 4 X 3 Y 12 19 4 Sarthaks Econnect Largest Online Education Community
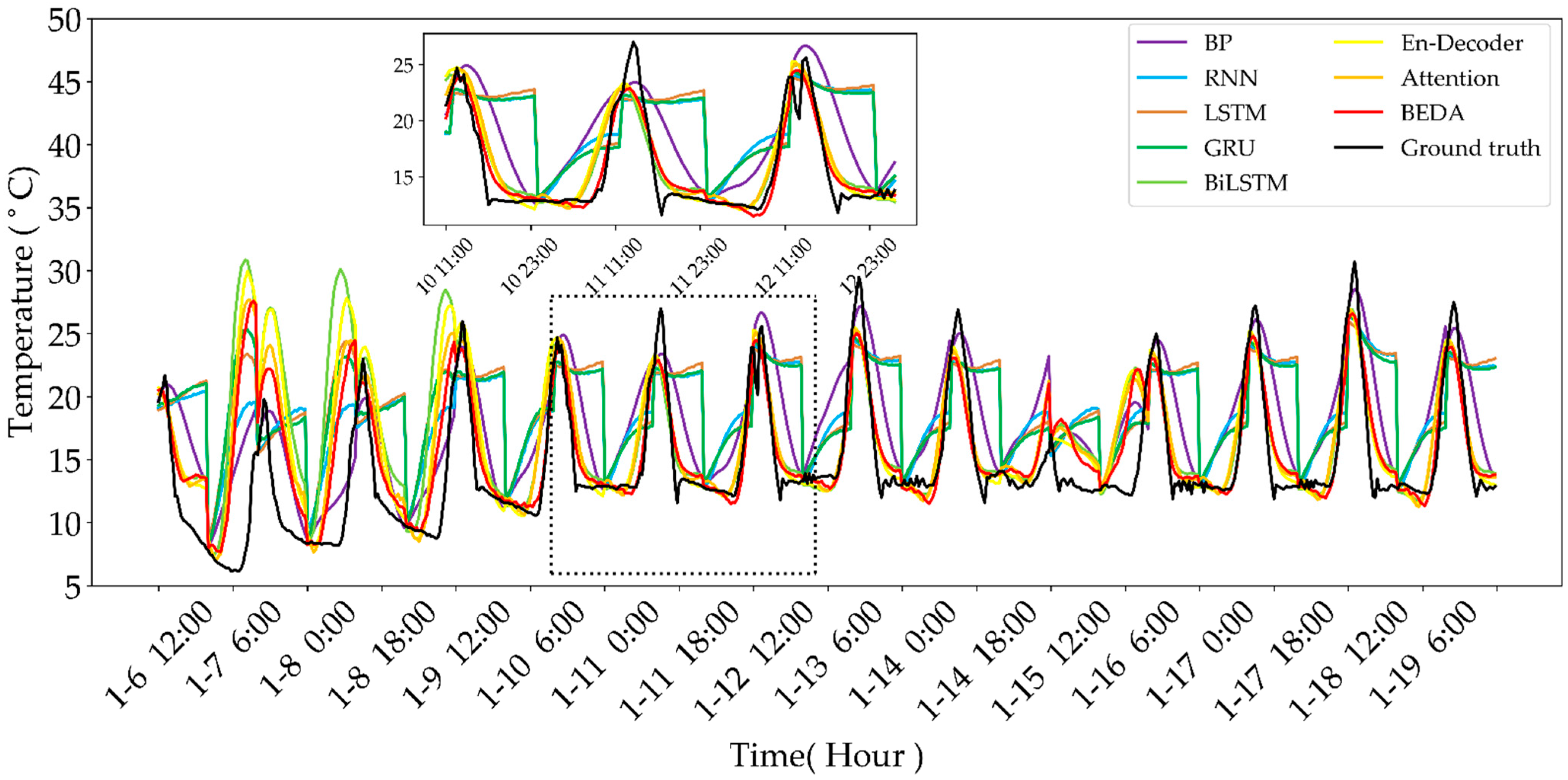



Agriculture Free Full Text Deep Learning Temporal Predictor Via Bidirectional Self Attentive Encoder Decoder Framework For Iot Based Environmental Sensing In Intelligent Greenhouse Html




1 2x 1 3y 21 1 3x 1 2y 13 6 Solve The Above Linear Equations By Reducing Them To A Pair Of Linear Equations Mathematics Topperlearning Com Snootk99



C1



1 2x 1 3y 21 1 3x 1 2y 13 6 Solve The Above Linear Equations By Reducing Them To A Pair Of Linear Equations Mathematics Topperlearning Com Snootk99




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3



Solve Each Of The Following Systems Of Equations By The Method Of Cross Multiplication 2x Y 6 0 X Y 2 0 Sarthaks Econnect Largest Online Education Community




Cross Multiplication Method For Solving Equations A Plus Topper




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y




Solve For X And Y Using Cross Multiplication Method 2 X 1 3 Y 1 2 3 X 1 2 Y 1 13 6 Maths Pair Of Linear Equations In Two Variables Meritnation Com



Solve The Following Systems Of Equations 1 2x 1 3y 2 1 3x 1 2y 13 6 Sarthaks Econnect Largest Online Education Community



Solve The System Of Equations By Using The Method Of Cross Multiplication 5 X Y 2 X Y 1 0 15 X Y 7 X Y 10 0 Sarthaks Econnect Largest Online Education Community
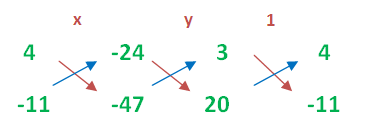



Solving Linear Equations Using Cross Multiplication Method




Ex 3 6 1 Iii Iv 4 X 3y 14 3 X 4y 23 Ex 3 6



Solve Each Of The Following Systems Of Equations By The Method Of Cross Multiplication X 2y 1 0 2x 3y 12 0 Sarthaks Econnect Largest Online Education Community




By Using Cross Multiplication Method Find X 2 2y 3 1 And X Y 3 3 Brainly In




Over 100 Data Scientist Interview Questions And Answers By Terence Shin Towards Data Science




Essd A 6 Year Long 13 18 High Resolution Air Quality Reanalysis Dataset In China Based On The Assimilation Of Surface Observations From Cnemc




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y
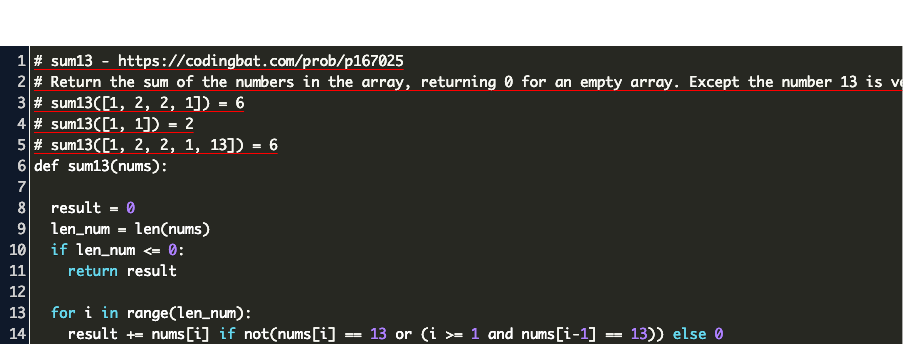



Sum13 Code Example
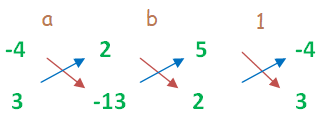



Solving Linear Equations Using Cross Multiplication Method




Chapter P Prerequisites Manualzz
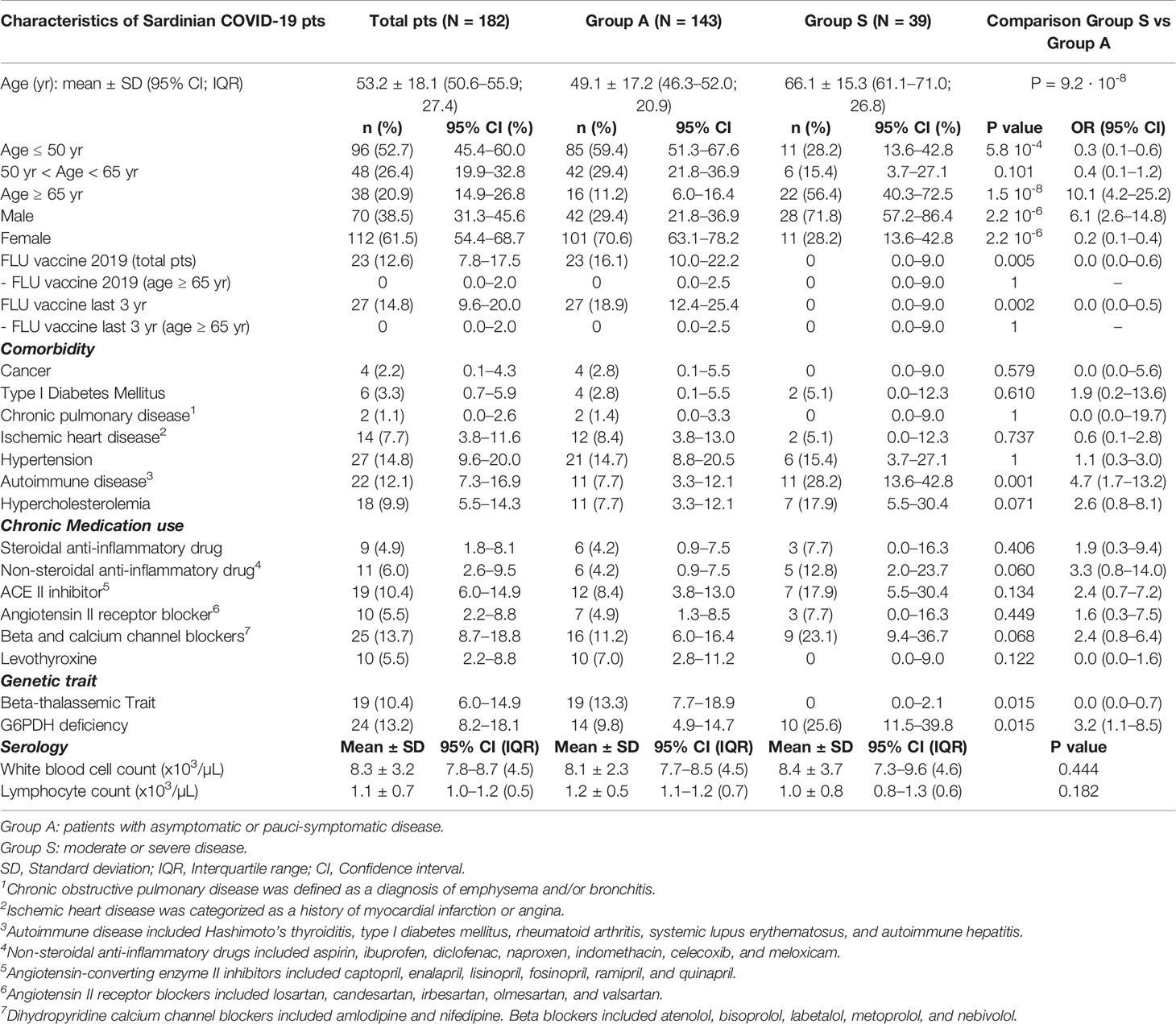



Frontiers Human Leukocyte Antigen Complex And Other Immunogenetic And Clinical Factors Influence Susceptibility Or Protection To Sars Cov 2 Infection And Severity Of The Disease Course The Sardinian Experience Immunology



1



C1




By Using Cross Multiplication Method Find X 2 2y 3 1 And X Y 3 3 Brainly In



2




Math 254h Old Assignments




Selina Solutions Class 9 Concise Maths Chapter 26 Co Ordinate Geometry Download Free Pdf




Glencoe Solution Manual
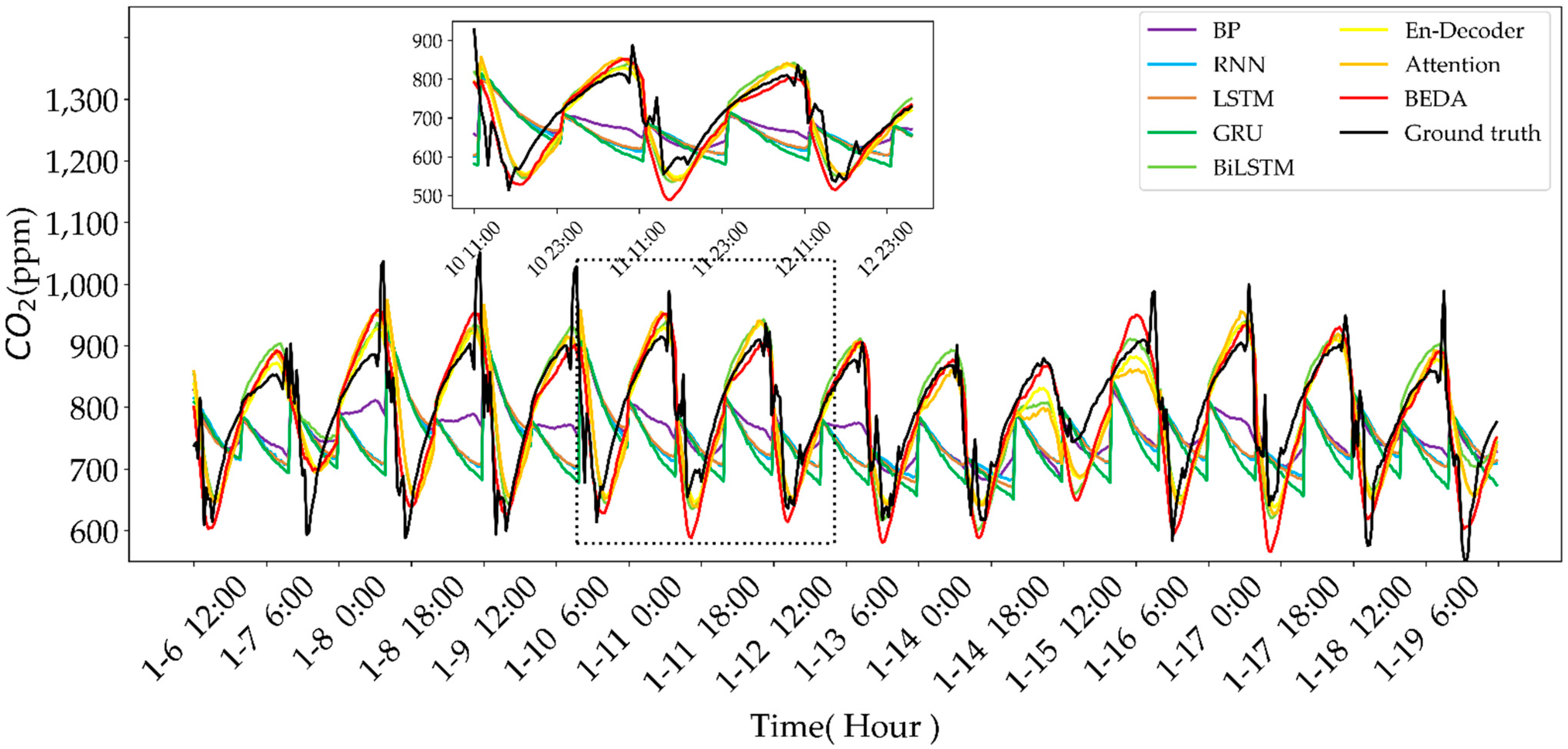



Agriculture Free Full Text Deep Learning Temporal Predictor Via Bidirectional Self Attentive Encoder Decoder Framework For Iot Based Environmental Sensing In Intelligent Greenhouse Html



C1




The Relationship Between Puberty And Social Emotion Processing Goddings 12 Developmental Science Wiley Online Library




Let F Be Differentiable For All X If F 1 2 And F X 2 For All Xepsilon 1 6 Then



C1




1 2x 1 3y 2 1 3x 1 2y 13 6 1 2x 1 3y 2 1 3x 1 2y 13 6 Rpk86 Youtube



Onlinepubs Trb Org




Class 10 Linear Equations In Two Variables 1 2x 1 3y 2 And 1 3x 1 2y 13 6 Ex 3 3 Q 16 Rd Sharma Youtube
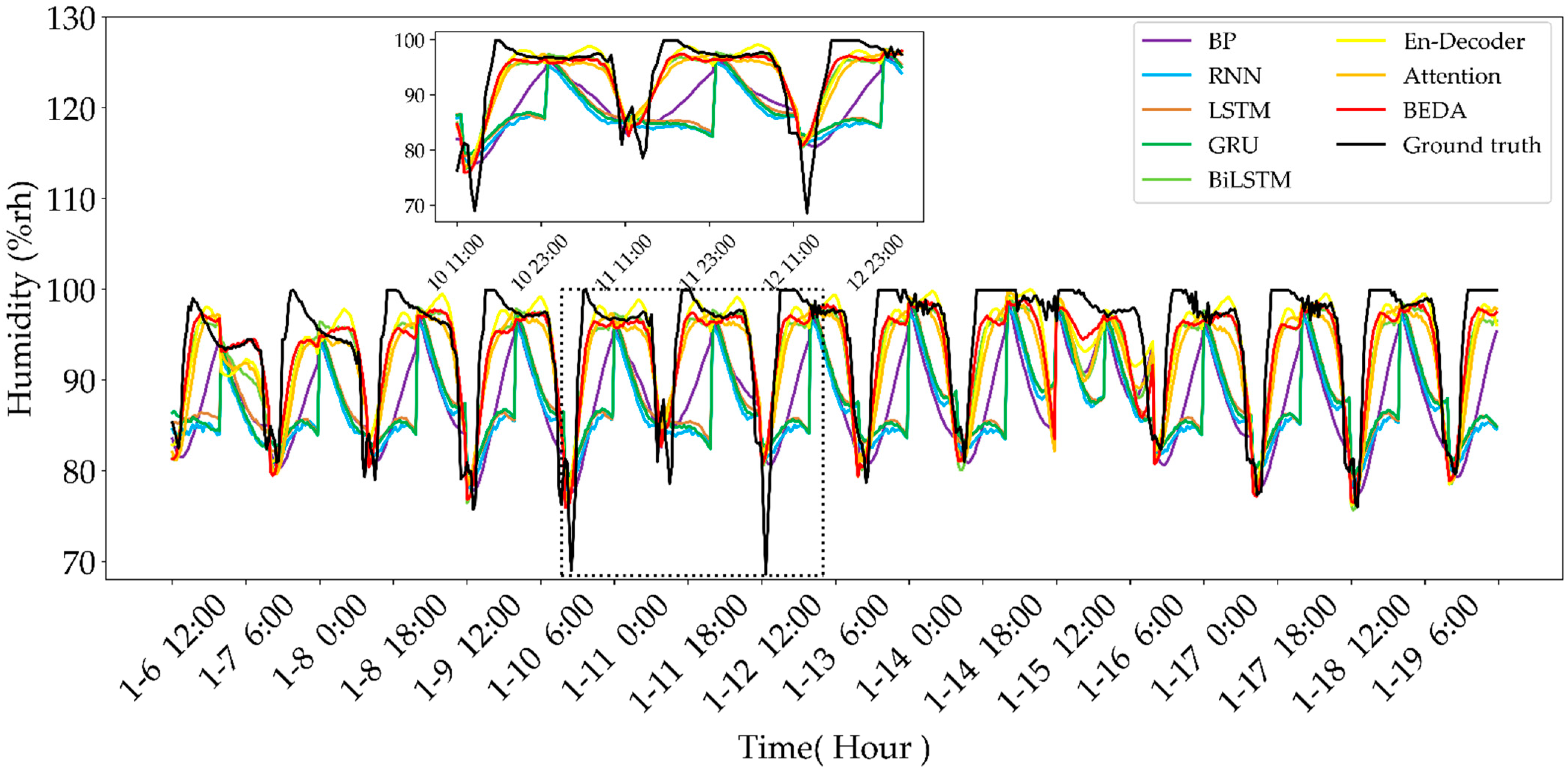



Agriculture Free Full Text Deep Learning Temporal Predictor Via Bidirectional Self Attentive Encoder Decoder Framework For Iot Based Environmental Sensing In Intelligent Greenhouse Html
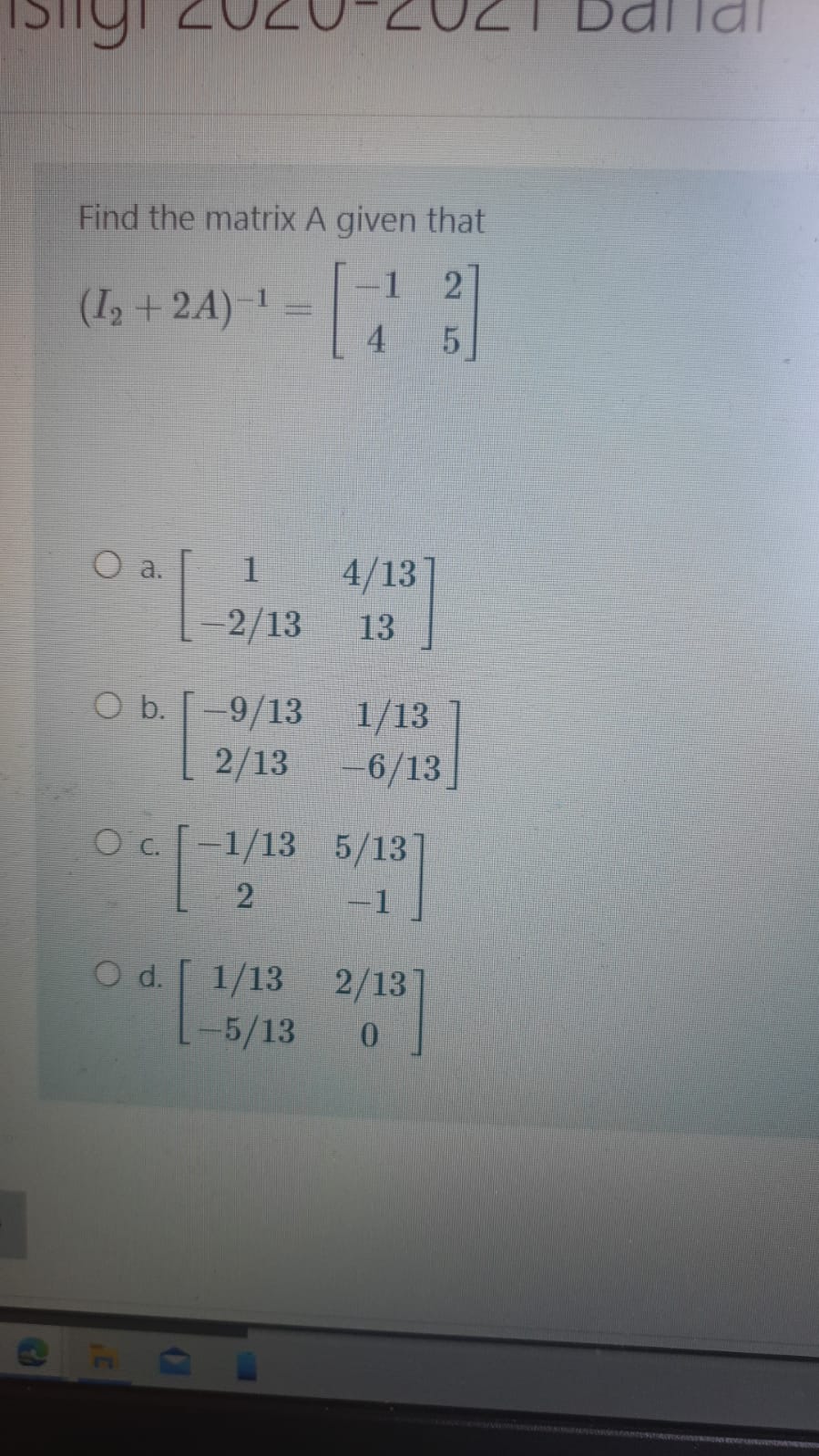



Answered Find The Matrix A Given That 1 2 I Bartleby




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y



Solving Linear Equations Using Cross Multiplication Method
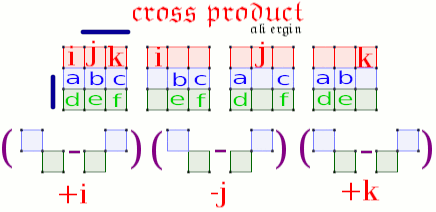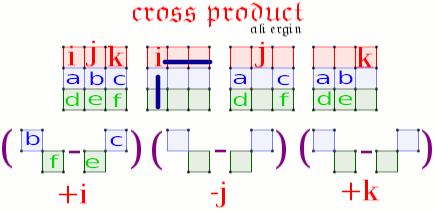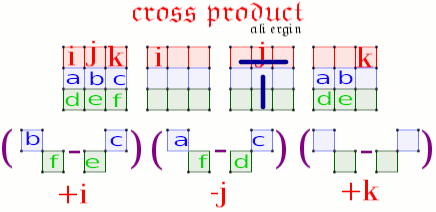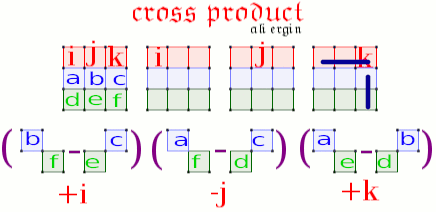



What Is The Cross Product Of 2 1 2 And 1 1 3 Socratic




3x 2 5y 3 2 And X 3 Y 2 13 6 Solve Using Substitution Method Youtube




Comparing Improper Fractions And Mixed Numbers Video Khan Academy




Solve For X And Y Using Cross Multiplication Method 2 X 1 3 Y 1 2 3 X 1 2 Y 1 13 6 Maths Pair Of Linear Equations In Two Variables Meritnation Com




Solved Consider The Following System Of Equations 10x1 Chegg Com
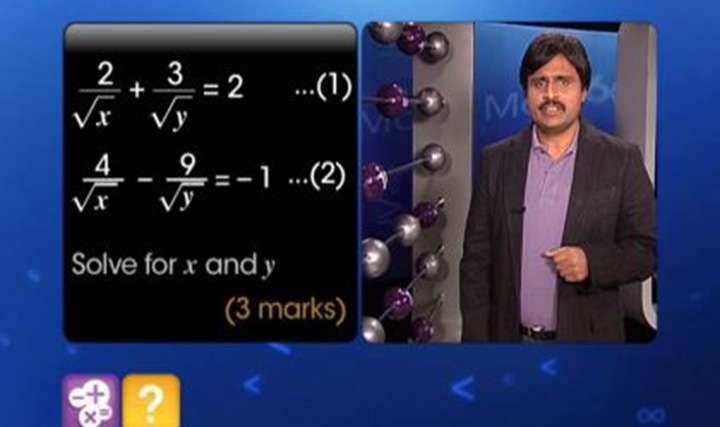



1 2x 1 3y 21 1 3x 1 2y 13 6 Solve The Above Linear Equations By Reducing Them To A Pair Of Linear Equations Mathematics Topperlearning Com Snootk99



Math 254h Old Assignments
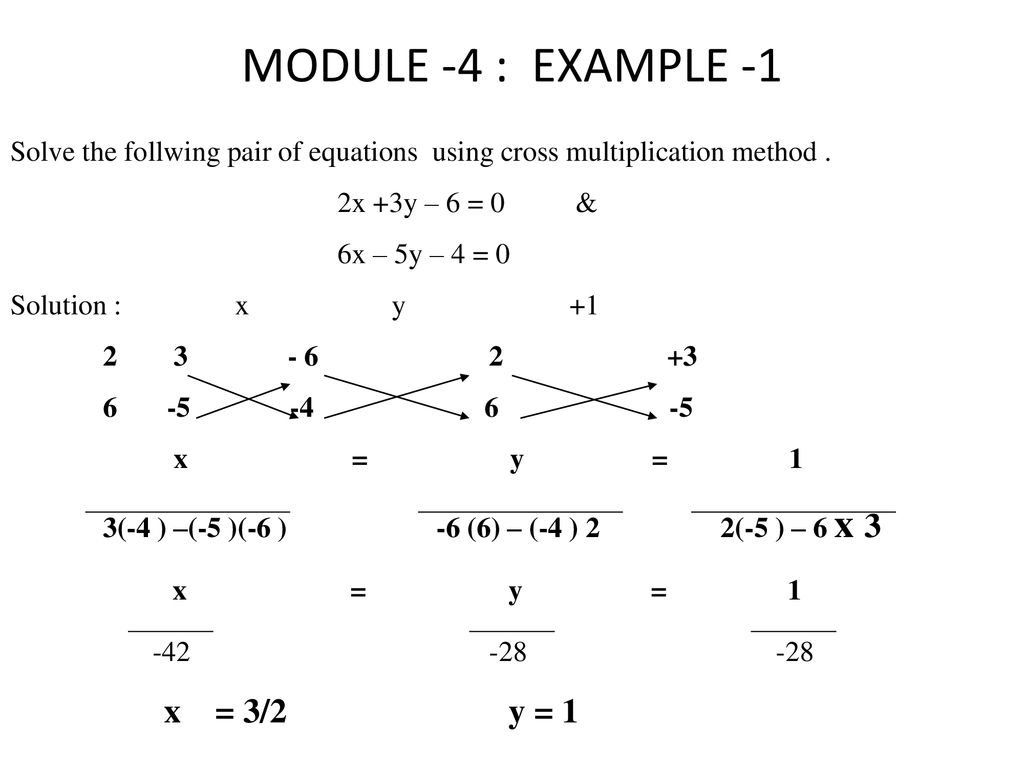



Topic Pair Of Linear Equtions In Two Variables Ppt Download




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y




Solve By Reducing Them To A Pair Of Linear Equations 5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Youtube




Example 18 Solve 5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Examples



1




Cross Multiplication Method For Solving Equations A Plus Topper



Solve The System Of Equations By Using The Method Of Cross Multiplication X 6 Y 15 4 0 X 3 Y 12 19 4 0 Sarthaks Econnect Largest Online Education Community
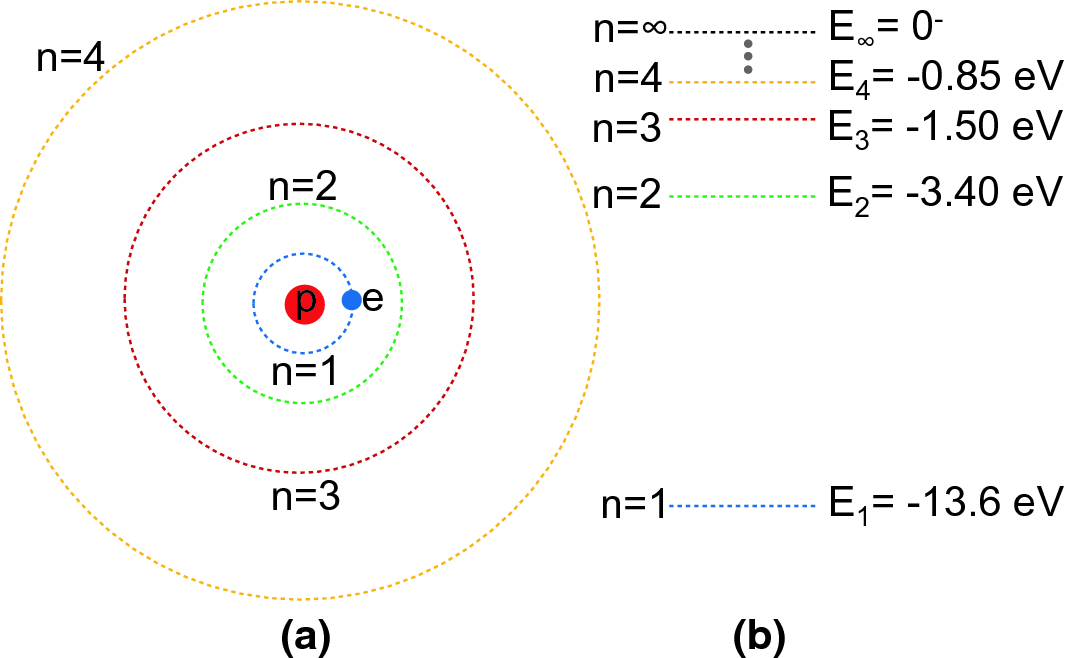



Electronic Structure Springerlink




Example 18 Solve 5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Examples




Solve X X 1 X 1 X 13 6 Brainly In




Esophageal Varices Noninvasive Diagnosis With Duplex Doppler Us In Patients With Compensated Cirrhosis Radiology
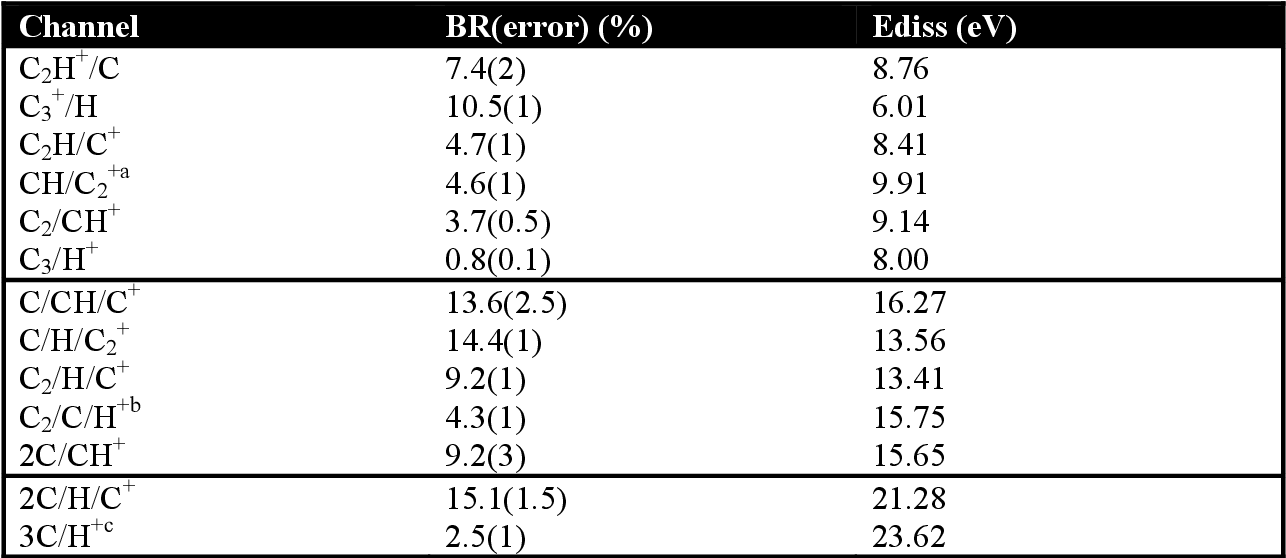



Pdf Fragmentation Branching Ratios Of Highly Excited Hydrocarbon Molecules Cnh And Their Cations Cnh N Lt Or 4 Semantic Scholar



7x 2y Xy 5 8x 7y Xy 15
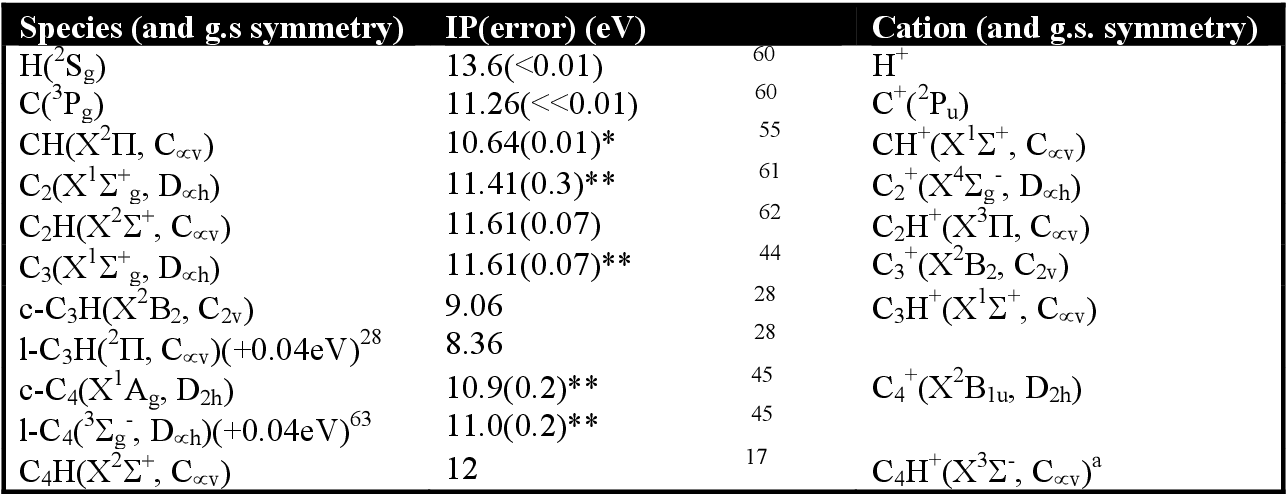



Pdf Fragmentation Branching Ratios Of Highly Excited Hydrocarbon Molecules Cnh And Their Cations Cnh N Lt Or 4 Semantic Scholar




Ex 3 6 1 Iii Iv 4 X 3y 14 3 X 4y 23 Ex 3 6




1 2x 1 3y 2 1 3x 1 2y 13 6 Solve The Pair Of Equations By Reducing Them To A Pair Of Linear Equation Youtube



0 件のコメント:
コメントを投稿